题目内容
设点M(x,y)到直线x=4的距离与它到定点(1,0)的距离之比为2,并记点M的轨迹曲线为C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设过定点(0,2)的直线l与曲线C交于不同的两点E,F,且∠EOF=90°(其中O为坐标原点),求直线l的斜率k的值;
(Ⅲ)设A(2,0),B(0,![]() )是曲线C的两个顶点,直线y=mx(m>0)与线段AB相交于点D,与椭圆相交于E,F两点.求四边形AEBF面积的最大值。
)是曲线C的两个顶点,直线y=mx(m>0)与线段AB相交于点D,与椭圆相交于E,F两点.求四边形AEBF面积的最大值。
解:(Ⅰ)设曲线![]() 上的任意一点
上的任意一点![]()
则有 化简得:
化简得:![]() …………………………4分
…………………………4分
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,与椭圆的交点
,与椭圆的交点![]()

![]()
![]()
![]()
![]()
![]() 或
或![]()
![]() ,
,![]() ……………………………………6分
……………………………………6分
因为![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 且
且![]() =90
=90![]() 得
得
![]() ,
,![]()
![]()
![]()
![]()
解得:![]() (满足
(满足![]() 或
或![]() )……………………………………8分
)……………………………………8分
(Ⅲ)  解方程组得
解方程组得 ;
;
即![]() ,
,![]()
![]() ………………………10分
………………………10分
![]()
![]()
![]()

因为![]() 所以
所以![]()
 (当且仅当
(当且仅当![]() 时取等号)
时取等号)
即![]() 的最大面积为
的最大面积为![]() (当
(当![]() 时取等号) …………………………12分
时取等号) …………………………12分

练习册系列答案
相关题目
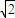 ,并记点M的轨迹为曲线C.
,并记点M的轨迹为曲线C.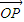 =
=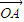 +
+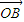 成立?若存在,求出直线l的方程;若不存在,说明理由.
成立?若存在,求出直线l的方程;若不存在,说明理由.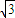 )是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.
)是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.