题目内容
设点M(x,y)到直线x=4的距离与它到定点(1,0)的距离之比为2,并记点M的轨迹曲线为C.(I)求曲线C的方程;
(II)设过定点(0,2)的直线l与曲线C交于不同的两点E,F,且∠EOF=90°(其中O为坐标原点),求直线l的斜率k的值;
(III)设A(2,0),B(0,
| 3 |
分析:(Ⅰ)设曲线C上的任意一点P(x,y),则有
=2,由此能求出曲线C的方程.
(Ⅱ)设直线l的方程为y=kx+2,与椭圆的交点E(x1,y1),F(x2,y2),由
,得(3+4k2)x2+16kx+4=0,再由根的判别式和l与椭圆交于不同的两点E,F且∠EOF=90°,得
•
=0,由此能够求出直线l的斜率k的值.
(Ⅲ)
解方程组得E(
,m
),F(-
,-m
),S四边形AEBF=2S△BOE+2S△FOA=|BO|•x1+|AO|•y1,由此能还应出S四边形AEBF的最大面积.
| |x-4| | ||
|
(Ⅱ)设直线l的方程为y=kx+2,与椭圆的交点E(x1,y1),F(x2,y2),由
|
| OE |
| OF |
(Ⅲ)
|
|
|
|
|
解答:解:(Ⅰ)设曲线C上的任意一点P(x,y)
则有
=2化简得:
+
=1(4分)
(Ⅱ)设直线l的方程为y=kx+2,与椭圆的交点E(x1,y1),F(x2,y2)
?(3+4k2)x2+16kx+4=0△=(16k)2-16(3+4k2)>0?k<-
或k>
x1+x2=-
,x1x2=
(6分)
因为l与椭圆交于不同的两点E,F且∠EOF=90°得
•
=0,x1x2+y1y2=0x1x2+(kx1+2)(kx2+2)=0(1+k2)x1x2+2k(x1+x2)+4=0
-
+4=0
解得:k=±
(满足k<-
或k>
)(8分)
(Ⅲ)
解方程组得
;
即E(
,m
),F(-
,-m
)S四边形AEBF=2S△BOE+2S△FOA=|BO|•x1+|AO|•y1(10分)=
+2m
=(
+2m)
=2
=2
)=2
因为4m+
≥4
所以2
≤2
(当且仅当m=
时取等号)
即S四边形AEBF的最大面积为2
(当m=
时取等号)(12分)
则有
| |x-4| | ||
|
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设直线l的方程为y=kx+2,与椭圆的交点E(x1,y1),F(x2,y2)
|
| 1 |
| 2 |
| 1 |
| 2 |
| 16k |
| 3+4k2 |
| 4 |
| 3+4k2 |
因为l与椭圆交于不同的两点E,F且∠EOF=90°得
| OE |
| OF |
| 4(1+k2) |
| 3+4k2 |
| 32k2 |
| 3+4k2 |
解得:k=±
2
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)
|
|
|
即E(
|
|
|
|
| 3 |
|
|
| 3 |
|
|
3(1+
|
3(1+
|
因为4m+
| 3 |
| m |
| 3 |
3(1+
|
| 6 |
| ||
| 2 |
即S四边形AEBF的最大面积为2
| 6 |
| ||
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
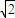 ,并记点M的轨迹为曲线C.
,并记点M的轨迹为曲线C.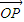 =
=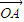 +
+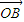 成立?若存在,求出直线l的方程;若不存在,说明理由.
成立?若存在,求出直线l的方程;若不存在,说明理由.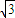 )是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.
)是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.