题目内容
设点M(x,y)到直线x=4的距离与它到定点(2,0)的距离之比为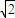 ,并记点M的轨迹为曲线C.
,并记点M的轨迹为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)过点(2,0)作直线l与曲线C相交于A、B两点,问C上是否存在点P,使得
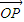 =
=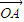 +
+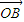 成立?若存在,求出直线l的方程;若不存在,说明理由.
成立?若存在,求出直线l的方程;若不存在,说明理由.
【答案】分析:(Ⅰ)由题意利用两点间的距离公式可得: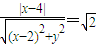 ,整理即可.
,整理即可.
(Ⅱ)设A(x1,y1),B(x2,y2),由题意知l的斜率一定不为0,故不妨设l:x=my+2.代入C的方程并整理得到根与系数的关系;假设存在点P,使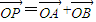 成立?点P的坐标(x1+x2,y1+y2)满足椭圆的方程.又A、B在椭圆上,即满足椭圆的方程.可得x1x2+2y1y2+4=0,代入解得m,即可得到点P的坐标.
成立?点P的坐标(x1+x2,y1+y2)满足椭圆的方程.又A、B在椭圆上,即满足椭圆的方程.可得x1x2+2y1y2+4=0,代入解得m,即可得到点P的坐标.
解答:解:(Ⅰ)由题意可得: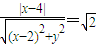 ,整理得C:
,整理得C: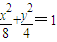 .
.
(Ⅱ)设A(x1,y1),B(x2,y2),由题意知l的斜率一定不为0,故不妨设l:x=my+2.
代入C的方程,并整理得(m2+2)y2+4my-4=0,显然△>0.
由韦达定理有: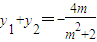 ,
,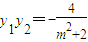 ,①
,①
假设存在点P,使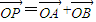 成立,则其充要条件为:
成立,则其充要条件为:
点P的坐标为(x1+x2,y1+y2),点P在椭圆上,即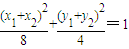 .
.
整理得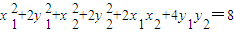 .
.
又A、B在椭圆上,即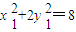 ,
,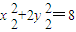 .
.
故x1x2+2y1y2+4=0 ②
将x1x2=(my1+2)(my2+2)=m2y1y2+2m(y1+y2)+4及①代入②解得m2=2.
∴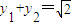 或
或 ,
,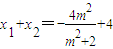 =2,即点P
=2,即点P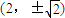 .
.
所以,存在点P,使得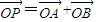 ,
,
这时直线l的方程为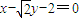 或
或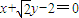 .
.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量的运算、两点间的距离公式等基本知识与基本技能,考查了分类讨论的思想方法、推理能力与计算能力..
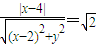 ,整理即可.
,整理即可.(Ⅱ)设A(x1,y1),B(x2,y2),由题意知l的斜率一定不为0,故不妨设l:x=my+2.代入C的方程并整理得到根与系数的关系;假设存在点P,使
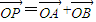 成立?点P的坐标(x1+x2,y1+y2)满足椭圆的方程.又A、B在椭圆上,即满足椭圆的方程.可得x1x2+2y1y2+4=0,代入解得m,即可得到点P的坐标.
成立?点P的坐标(x1+x2,y1+y2)满足椭圆的方程.又A、B在椭圆上,即满足椭圆的方程.可得x1x2+2y1y2+4=0,代入解得m,即可得到点P的坐标.解答:解:(Ⅰ)由题意可得:
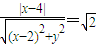 ,整理得C:
,整理得C: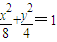 .
.(Ⅱ)设A(x1,y1),B(x2,y2),由题意知l的斜率一定不为0,故不妨设l:x=my+2.
代入C的方程,并整理得(m2+2)y2+4my-4=0,显然△>0.
由韦达定理有:
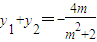 ,
,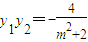 ,①
,①假设存在点P,使
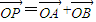 成立,则其充要条件为:
成立,则其充要条件为:点P的坐标为(x1+x2,y1+y2),点P在椭圆上,即
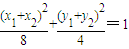 .
.整理得
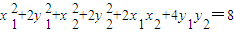 .
.又A、B在椭圆上,即
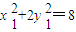 ,
,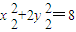 .
.故x1x2+2y1y2+4=0 ②
将x1x2=(my1+2)(my2+2)=m2y1y2+2m(y1+y2)+4及①代入②解得m2=2.
∴
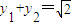 或
或 ,
,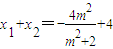 =2,即点P
=2,即点P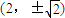 .
. 所以,存在点P,使得
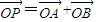 ,
,这时直线l的方程为
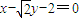 或
或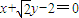 .
.点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量的运算、两点间的距离公式等基本知识与基本技能,考查了分类讨论的思想方法、推理能力与计算能力..

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
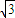 )是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.
)是曲线C的两个顶点,直线y=mx(x>0)与线段AB相交于点D,与椭圆相交于E,F两点,求四边形AEBF面积的最大值.