题目内容
过抛物线 的焦点的直线
的焦点的直线 与抛物线交于
与抛物线交于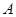 、
、 两点,且
两点,且 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,则
,则 = .
= .
 的焦点的直线
的焦点的直线 与抛物线交于
与抛物线交于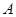 、
、 两点,且
两点,且 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,则
,则 = .
= .
试题分析:先根据抛物线的方程求得焦点的坐标,代入直线方程求得
 和
和 的关系式,进而把直线与抛物线方程联立消去
的关系式,进而把直线与抛物线方程联立消去 ,求得方程的解,进而根据直线方程可分别求得
,求得方程的解,进而根据直线方程可分别求得 和
和 ,
, 的面积可分为
的面积可分为 与
与 的面积之和,而
的面积之和,而 与
与 若以
若以 为公共底,则其高即为
为公共底,则其高即为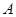 、
、 两点的
两点的 轴坐标的绝对值,进而可表示三角形的面积进而求得
轴坐标的绝对值,进而可表示三角形的面积进而求得 ,则
,则 的值可得,代入
的值可得,代入 中,即可求得答案.
中,即可求得答案.
练习册系列答案
相关题目
 +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为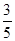 .
.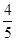 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标. +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距. (
(  )的离心率为
)的离心率为 ,点(1,
,点(1, )在椭圆C上.
)在椭圆C上. ),其中
),其中 ,切点分别是A、B,试利用结论:在椭圆
,切点分别是A、B,试利用结论:在椭圆 )处的椭圆切线方程是
)处的椭圆切线方程是 ,证明直线AB恒过椭圆的右焦点
,证明直线AB恒过椭圆的右焦点 ;
; 的值是否恒为常数,若是,求出此常数;若不是,请说明理由.
的值是否恒为常数,若是,求出此常数;若不是,请说明理由. 上的点M与椭圆右焦点
上的点M与椭圆右焦点 的连线
的连线 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
 的面积是
的面积是 ,求此时椭圆的方程.
,求此时椭圆的方程. +y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )
+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( )


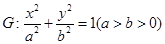 过点
过点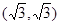 ,且离心率为
,且离心率为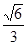 .斜率为
.斜率为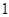 的直线
的直线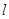 与椭圆
与椭圆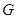 交于
交于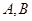 两点,以
两点,以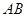 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为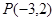 .
.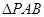 的面积.
的面积. 的右焦点重合,则该抛物线的准线方程为___________.
的右焦点重合,则该抛物线的准线方程为___________. 经过点
经过点 ,离心率
,离心率 ,直线
,直线 与椭圆交于
与椭圆交于 ,
, 两点,向量
两点,向量
 ,
,
 ,且
,且 .
. (
(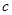 为半焦距)时,求直线
为半焦距)时,求直线 .
.