题目内容
设A,B分别为椭圆 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
(1)求椭圆的方程;
(2)设P(4,x)(x≠0),若直线AP,BP分别与椭圆相交于异于A,B的点M,N,求证:∠MBN为钝角.
 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.(1)求椭圆的方程;
(2)设P(4,x)(x≠0),若直线AP,BP分别与椭圆相交于异于A,B的点M,N,求证:∠MBN为钝角.
(1) +
+ =1 (2)见解析
=1 (2)见解析
 +
+ =1 (2)见解析
=1 (2)见解析(1)依题意,得a=2c,b2=a2-c2=3c2,
设椭圆方程为 +
+ =1,将(1,
=1,将(1, )代入,得c2=1,故椭圆方程为
)代入,得c2=1,故椭圆方程为 +
+ =1.
=1.
(2)证明:由(1),知A(-2,0),B(2,0),
设M(x0,y0),则-2<x0<2,y02= (4-x02),由P,A,M三点共线,得x=
(4-x02),由P,A,M三点共线,得x= ,
, =(x0-2,y0),
=(x0-2,y0), =(2,
=(2, ),
), ·
· =2x0-4+
=2x0-4+ =
= (2-x0)>0,
(2-x0)>0,
即∠MBP为锐角,则∠MBN为钝角.
设椭圆方程为
 +
+ =1,将(1,
=1,将(1, )代入,得c2=1,故椭圆方程为
)代入,得c2=1,故椭圆方程为 +
+ =1.
=1.(2)证明:由(1),知A(-2,0),B(2,0),
设M(x0,y0),则-2<x0<2,y02=
 (4-x02),由P,A,M三点共线,得x=
(4-x02),由P,A,M三点共线,得x= ,
, =(x0-2,y0),
=(x0-2,y0), =(2,
=(2, ),
), ·
· =2x0-4+
=2x0-4+ =
= (2-x0)>0,
(2-x0)>0,即∠MBP为锐角,则∠MBN为钝角.

练习册系列答案
相关题目
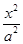 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
. ,求斜率k的值;
,求斜率k的值;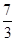 ,0),求证:
,0),求证: ·
· 为定值.
为定值. ,一条准线的方程是x=2
,一条准线的方程是x=2

 =
= +2
+2 ,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣
,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣ ,
, 的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.
的距离之比为定值;若存在,求F的坐标,若不存在,说明理由. :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 的形状是( )
的形状是( ) +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( ) )
) 的焦点的直线
的焦点的直线 与抛物线交于
与抛物线交于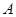 、
、 两点,且
两点,且 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,则
,则 = .
= . 为坐标原点,双曲线
为坐标原点,双曲线 和椭圆
和椭圆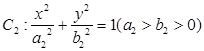 均过点
均过点 ,且以
,且以 的两个顶点和
的两个顶点和 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形. 的方程;
的方程; ,使得
,使得 两点,与
两点,与 ?证明你的结论.
?证明你的结论.