题目内容
17.函数y=x2+$\frac{3}{x}$(x>0)的最小值是$\frac{3\root{3}{18}}{2}$.分析 由x2+$\frac{3}{x}$=x2+$\frac{3}{2x}$+$\frac{3}{2x}$,根据均值不等式即可求出最小值.
解答 解:y=x2+$\frac{3}{x}$=x2+$\frac{3}{2x}$+$\frac{3}{2x}$≥3$\root{3}{{x}^{2}•\frac{3}{2x}•\frac{3}{2x}}$=$\frac{3\root{3}{18}}{2}$,当且仅当x2=$\frac{3}{2x}$,即x=$\frac{\root{3}{12}}{2}$时取等号,
故函数y=x2+$\frac{3}{x}$(x>0)的最小值是$\frac{3\root{3}{18}}{2}$.
故答案为:$\frac{3\root{3}{18}}{2}$.
点评 本题考查了均值不等式的应用,关键是转化,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
7.已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=3,且(3+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为( )
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{5}{4}$$\sqrt{3}$ | D. | $\frac{9}{4}$$\sqrt{3}$ |
8.若函数f(x)=x2+6x,则函数f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数也不是偶函数 |
9.已知集合A={x|(x2-5x+6)(x2-12x+35)=0},集合B是元素小于10的质数,则集合A与B的关系为( )
| A. | A=B | B. | A?B | C. | B?A | D. | A?B |
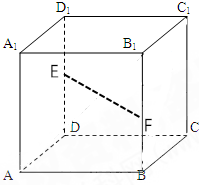 如图,在正方体ABCD-A1B1C1D1中,点E是DD1的中点,点F是BB1的中点.求证:EF∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,点E是DD1的中点,点F是BB1的中点.求证:EF∥平面ABCD.