题目内容
已知函数f(x)的导函数为f′(x),且对任意x>0,都有f′(x)>
.
(Ⅰ)判断函数F(x)=
在(0,+∞)上的单调性;
(Ⅱ)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)请将(Ⅱ)中的结论推广到一般形式,并证明你所推广的结论.
| f(x) |
| x |
(Ⅰ)判断函数F(x)=
| f(x) |
| x |
(Ⅱ)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)请将(Ⅱ)中的结论推广到一般形式,并证明你所推广的结论.
考点:利用导数研究函数的单调性
专题:函数的性质及应用
分析:(Ⅰ)求出导数F'(x),根据条件判断导数在(0,+∞)内的符号,从而说明函数F(x)的单调性;
(Ⅱ)运用(Ⅰ)的结论证明,注意应用累加法;
(Ⅲ)先写出推广的结论,然后运用(Ⅰ)的结论证明,并注意累加.
(Ⅱ)运用(Ⅰ)的结论证明,注意应用累加法;
(Ⅲ)先写出推广的结论,然后运用(Ⅰ)的结论证明,并注意累加.
解答:
解:(Ⅰ)对F(x)求导数,得F′(x)=
,
∵f′(x)>
,x>0,∴xf′(x)>f(x),即xf′(x)-f(x)>0,
∴F′(x)>0,
故F(x)=
在(0,+∞)上是增函数;
(Ⅱ)∵x1>0,x2>0,∴0<x1<x1+x2.
由(Ⅰ),知F(x)=
在(0,+∞)上是增函数,
∴F(x1)<F(x1+x2),即
<
,
∵x1>0,∴f(x1)<
f(x1+x2),
同理可得f(x2)<
f(x1+x2),
以上两式相加,得f(x1)+f(x2)<f(x1+x2);
(Ⅲ)(Ⅱ)中结论的推广形式为:
设x1,x2,…,xn∈(0,+∞),其中n≥2,则f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).
∵x1>0,x2>0,…,xn>0,
∴0<x1<x1+x2+…+xn.
由(Ⅰ),知F(x)=
在(0,+∞)上是增函数,
∴F(x1)<F(x1+x2+…+xn),即
<
.
∵x1>0,
∴f(x1)<
f(x1+x2+…+xn).
同理可得
f(x2)<
f(x1+x2+…+xn),
f(x3)<
f(x1+x2+…+xn),
…
f(xn)<
f(x1+x2+…+xn),
以上n个不等式相加,得f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).
| xf′(x)-f(x) |
| x2 |
∵f′(x)>
| f(x) |
| x |
∴F′(x)>0,
故F(x)=
| f(x) |
| x |
(Ⅱ)∵x1>0,x2>0,∴0<x1<x1+x2.
由(Ⅰ),知F(x)=
| f(x) |
| x |
∴F(x1)<F(x1+x2),即
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
∵x1>0,∴f(x1)<
| x1 |
| x1+x2 |
同理可得f(x2)<
| x2 |
| x1+x2 |
以上两式相加,得f(x1)+f(x2)<f(x1+x2);
(Ⅲ)(Ⅱ)中结论的推广形式为:
设x1,x2,…,xn∈(0,+∞),其中n≥2,则f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).
∵x1>0,x2>0,…,xn>0,
∴0<x1<x1+x2+…+xn.
由(Ⅰ),知F(x)=
| f(x) |
| x |
∴F(x1)<F(x1+x2+…+xn),即
| f(x1) |
| x1 |
| f(x1+x2+…+xn) |
| x1+x2+…+xn |
∵x1>0,
∴f(x1)<
| x1 |
| x1+x2+…+xn |
同理可得
f(x2)<
| x2 |
| x1+x2+…+xn |
f(x3)<
| x3 |
| x1+x2+…+xn |
…
f(xn)<
| xn |
| x1+x2+…+xn |
以上n个不等式相加,得f(x1)+f(x2)+…+f(xn)<f(x1+x2+…+xn).
点评:本题考查导数的一个应用--求函数的单调性,同时重点考查函数单调性及应用,考查推理能力,是一道中档题.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
A、
| ||
B、
| ||
| C、π | ||
D、
|
设双曲线F:
-
=1(a>0,b>0),F1,F2为双曲线F的焦点.若双曲线F存在点M,满足
|MF1|=|MO|=|MF2|(O为原点),则双曲线F的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙、丙、丁、戊五人并排站成一排,如果甲必须站在乙的右边(甲、乙可以不相邻)那么不同的排法共有( )
| A、24种 | B、60种 |
| C、90种 | D、120种 |
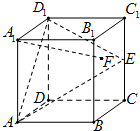 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是