题目内容
设函数f(x)=sin xcos x-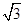 cos(π+x)cos x(x∈R).
cos(π+x)cos x(x∈R).
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b=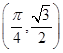 平移后得到函数y=g(x)的图象,求y=g(x)在[0,
平移后得到函数y=g(x)的图象,求y=g(x)在[0,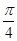 ]上的最大值.
]上的最大值.
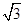 cos(π+x)cos x(x∈R).
cos(π+x)cos x(x∈R).(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b=
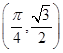 平移后得到函数y=g(x)的图象,求y=g(x)在[0,
平移后得到函数y=g(x)的图象,求y=g(x)在[0,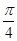 ]上的最大值.
]上的最大值.(1)π (2)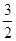
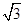
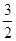
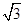
(1)f(x)=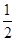 sin 2x+
sin 2x+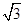 cos2x
cos2x
=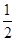 sin 2x+
sin 2x+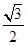 (1+cos 2x)
(1+cos 2x)
=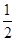 sin 2x+
sin 2x+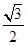 cos 2x+
cos 2x+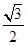
=sin(2x+ )+
)+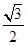 .
.
故f(x)的最小正周期为T=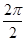 =π.
=π.
(2)依题意g(x)=f(x-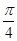 )+
)+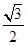
=sin [2(x-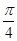 )+
)+ ]+
]+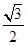 +
+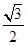
=sin (2x-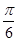 )+
)+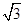 .
.
当x∈[0,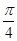 ]时,2x-
]时,2x-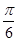 ∈[-
∈[-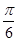 ,
, ],g(x)为增函数,所以g(x)在[0,
],g(x)为增函数,所以g(x)在[0,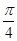 ]上的最大值为g(
]上的最大值为g(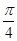 )=
)=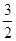
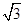 .
.
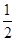 sin 2x+
sin 2x+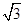 cos2x
cos2x=
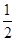 sin 2x+
sin 2x+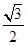 (1+cos 2x)
(1+cos 2x)=
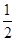 sin 2x+
sin 2x+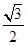 cos 2x+
cos 2x+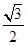
=sin(2x+
 )+
)+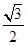 .
.故f(x)的最小正周期为T=
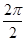 =π.
=π.(2)依题意g(x)=f(x-
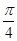 )+
)+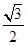
=sin [2(x-
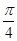 )+
)+ ]+
]+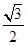 +
+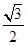
=sin (2x-
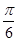 )+
)+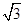 .
.当x∈[0,
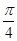 ]时,2x-
]时,2x-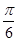 ∈[-
∈[-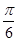 ,
, ],g(x)为增函数,所以g(x)在[0,
],g(x)为增函数,所以g(x)在[0,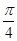 ]上的最大值为g(
]上的最大值为g(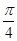 )=
)=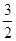
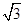 .
.
练习册系列答案
相关题目
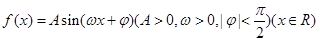 的部分图象如图所示.
的部分图象如图所示.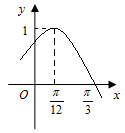
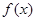 的表达式;
的表达式;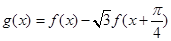 ,求函数
,求函数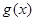 的最小值及相应的
的最小值及相应的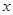 的取值集合.
的取值集合.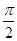 )内递增的是( )
)内递增的是( )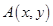 在圆
在圆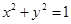 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间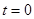 时,
时, 坐标是
坐标是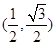 ,则当
,则当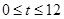 时,动点
时,动点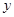 关于
关于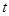 (秒)的函数的单调递增区间是( )
(秒)的函数的单调递增区间是( )


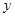 轴上的角的集合是
轴上的角的集合是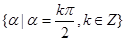 ;
;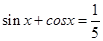 ,则
,则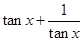 的值为
的值为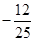 ;
;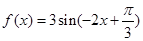 在区间
在区间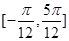 内是减函数;
内是减函数;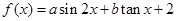 ,且
,且 ,则
,则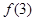 的值为
的值为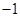 ;
;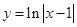 的图像与函数
的图像与函数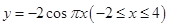 的图像所有交点的横坐标之和等于6.
的图像所有交点的横坐标之和等于6.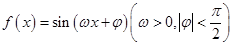 的部分图象如图所示.
的部分图象如图所示. 的解析式,并写出
的解析式,并写出 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且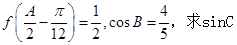 的值.
的值.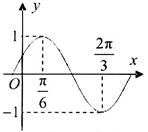
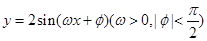 的图象上的一段,则( )
的图象上的一段,则( )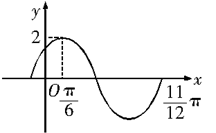

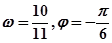


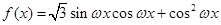 ,
,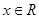 ,
,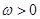 .
.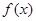 的值域;
的值域; 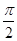 ,则当
,则当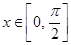 时,求
时,求