题目内容
给出下列说法:
①终边在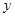 轴上的角的集合是
轴上的角的集合是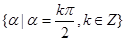 ;
;
②若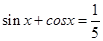 ,则
,则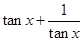 的值为
的值为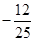 ;
;
③函数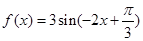 在区间
在区间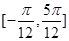 内是减函数;
内是减函数;
④若函数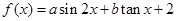 ,且
,且 ,则
,则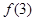 的值为
的值为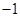 ;
;
⑤函数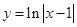 的图像与函数
的图像与函数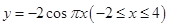 的图像所有交点的横坐标之和等于6.
的图像所有交点的横坐标之和等于6.
其中正确的说法是 .(写出所有正确说法的序号)
①终边在
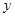 轴上的角的集合是
轴上的角的集合是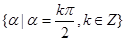 ;
;②若
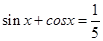 ,则
,则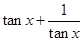 的值为
的值为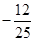 ;
;③函数
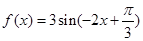 在区间
在区间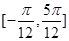 内是减函数;
内是减函数;④若函数
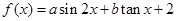 ,且
,且 ,则
,则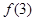 的值为
的值为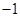 ;
;⑤函数
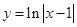 的图像与函数
的图像与函数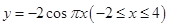 的图像所有交点的横坐标之和等于6.
的图像所有交点的横坐标之和等于6.其中正确的说法是 .(写出所有正确说法的序号)
③④⑤
①终边在
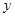 轴上的角的集合是
轴上的角的集合是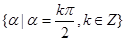 是错误的,当
是错误的,当 时
时 ,终边在
,终边在 轴上;
轴上;②由
 或
或 ,故
,故 或
或 则
则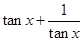 的值为
的值为 ,故 ②错; ③函数
,故 ②错; ③函数 的单调递减区间是
的单调递减区间是 当
当 时即为
时即为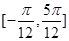 ,所以③正确;④注意到函数
,所以③正确;④注意到函数 为奇函数,则
为奇函数,则 则
则 ,故④正确;⑤在同一坐标系中作出
,故④正确;⑤在同一坐标系中作出 与
与 的图像如图,又
的图像如图,又 的周期为2,两图象都关于直线x=1对称,且共有6个交点,由中点坐标公式可得:
的周期为2,两图象都关于直线x=1对称,且共有6个交点,由中点坐标公式可得: ,故所有交点的横坐标之和为6,故⑤正确
,故所有交点的横坐标之和为6,故⑤正确
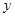 轴上的角的集合,同角三角函数基本关系式,奇函数,正弦函数的单调区间,函数图像的对称性,中点坐标公式
轴上的角的集合,同角三角函数基本关系式,奇函数,正弦函数的单调区间,函数图像的对称性,中点坐标公式
练习册系列答案
相关题目
 .
. 在一个周期内的图像
在一个周期内的图像 上的最大值和最小值.
上的最大值和最小值.
 (1)求函数的周期;(2)求函数的单调递增区间;(3)若
(1)求函数的周期;(2)求函数的单调递增区间;(3)若 时,
时, 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值. cos(π+x)cos x(x∈R).
cos(π+x)cos x(x∈R). 平移后得到函数y=g(x)的图象,求y=g(x)在[0,
平移后得到函数y=g(x)的图象,求y=g(x)在[0,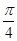 ]上的最大值.
]上的最大值. ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m. ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S. 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 个单位,得到的图象对应的僻析式是( )
个单位,得到的图象对应的僻析式是( )



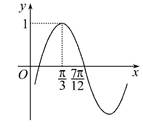
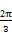
 的最小正周期和振幅分别是( )
的最小正周期和振幅分别是( ) ,1
,1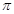 ,1
,1 的部分图象如图所示,则
的部分图象如图所示,则 ( )
( )



