题目内容
下列命题正确的个数( )(1)命题“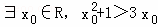 ”的否定是“∀x∈R,x2+1≤3x”;
”的否定是“∀x∈R,x2+1≤3x”;
(2)函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
(3)“x2+2x≥ax在x∈[1,2]上恒成立”⇔“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立”
(4)“平面向量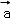 与
与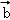 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“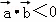 ”A. 1 B. 2 C. 3 D. 4
”A. 1 B. 2 C. 3 D. 4
B解答: 解:(1)根据特称命题的否定是全称命题,∴(1)正确;
(2)f(x)= ﹣
﹣ =cos2ax,最小正周期是
=cos2ax,最小正周期是 =π⇒a=±1,∴(2)正确;
=π⇒a=±1,∴(2)正确;
(3)例a=2时,x2+2x≥2x在x∈[1,2]上恒成立,而(x2+2x)min=3<2xmax=4,∴(3)不正确;
(4)∵ •
• =|
=| ||
|| |cos
|cos ,∵
,∵ =π时
=π时 <0,∴(4)错误.故选B
<0,∴(4)错误.故选B

练习册系列答案
相关题目
若 ,
, ,
, 均为单位向量,且
均为单位向量,且 ,
, ,则
,则 的最大值为( )
的最大值为( )
|
| A. |
| B. | 1 | C. |
| D. | 2 |
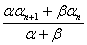 ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0.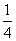 , a1=1,a2=
, a1=1,a2=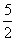 ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+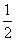 } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项. 
 的前
的前
 项和
项和 ,正项等比数列
,正项等比数列
 中,
中, ,
, ,则
,则 ( )
( )
 B.
B.
 C.
C.
 D.
D.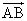 =λa+b,
=λa+b,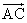 =a+μb(λ,μ∈R),那么A、B、C三点共线的充要条件为( )
=a+μb(λ,μ∈R),那么A、B、C三点共线的充要条件为( ) 的边长为
的边长为 ,平面内一点
,平面内一点 满足
满足 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.


 的中心为点
的中心为点 ,
, 为平面内任意一点,则
为平面内任意一点,则 ( )
( ) B.
B. C.3
C.3 中,点
中,点 在线段
在线段 上, 点
上, 点 在线段
在线段 上且满足
上且满足 ,若
,若 ,则
,则 的值为A.
的值为A. B.
B. C.
C. D.
D.

 ,
, .若
.若 使
使 则角C的大小为
则角C的大小为 B.
B.  C.
C.  D.
D. 