题目内容
1.我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是6万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度x(厘米)满足关系式:C(x)=$\frac{k}{3x+8}$(0≤x≤10),若无隔热层(即x=0),则每年能源消耗费用为5万元.设f(x)为隔热层建造费用与使用20年的能源消耗费用之和.(1)求C(x)和f(x)的表达式;
(2)当隔热层修建多少厘米厚时,总费用f(x)最小,并求出最小值.
分析 (1)根据关系式:C(x)=$\frac{k}{3x+8}$(0≤x≤10),无隔热层,则每年能源消耗费用为5万元,可求C(x),利用f(x)为隔热层建造费用与使用20年的能源消耗费用之和,可求函数关系式;
(2)利用基本不等式,即可求得函数的最小值.
解答 解:(1)当x=0时,C=5,因为C(x)=$\frac{k}{3x+8}$(0≤x≤10),所以k=40,故C(x)=$\frac{40}{3x+8}$…(3分)
∵f(x)为隔热层建造费用与使用20年的能源消耗费用之和
∴f(x)=6x+20×$\frac{40}{3x+8}$(0≤x≤10).…(6分)
(2)f(x)=6x+20×$\frac{40}{3x+8}$=2(3x+8)+20×$\frac{40}{3x+8}$-16≥2$\sqrt{1600}$-16=64,…(9分)
当且仅当2(3x+8)=20×$\frac{40}{3x+8}$,
即x=4时取得最小值.…(11分)
即隔热层修建4厘米厚时,总费用达到最小值,最小值为64万元.…(12分)
点评 本题考查函数模型的构建,考查利用基本不等式求函数的最值,考查学生的阅读能力,建立函数模型是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.“指数函数y=ax(a>0且a≠1)是减函数,y=3x是指数函数,所以y=3x是减函数”你认为这个推理( )
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 推理形式错误 |
10.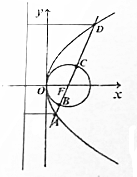 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |