题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{x-\frac{1}{x},x≥2}\\{x,x<2}\end{array}\right.$,若使不等式f(x)<$\frac{8}{3}$成立,则x的取值范围为{x|x<3}.分析 根据函数的表达式解关于x≥2时的不等式f(x)<$\frac{8}{3}$即可.
解答 解:∴f(x)=$\left\{\begin{array}{l}{x-\frac{1}{x},x≥2}\\{x,x<2}\end{array}\right.$,
∴x<2时,不等式f(x)<$\frac{8}{3}$恒成立,
x≥2时,x-$\frac{1}{x}$<$\frac{8}{3}$,解得:2≤x<3,
综上,不等式的解集是:{x|x<3},
故答案为:{x|x<3}.
点评 本题考查了分段函数问题,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
3.“e是无限不循环小数,所以e为无理数.”该命题是演绎推理中的三段论推理,其中大前提是( )
| A. | 无理数是无限不循环小数 | B. | 有限小数或有限循环小数为有理数 | ||
| C. | 无限不循环小数是无理数 | D. | 无限小数为无理数 |
10.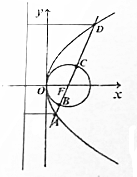 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
7.为了分析某次考试数学成绩情况,用简单随机抽样从某班中抽取40名学生的成绩作为样本,得到频率分布表如表:
(Ⅰ)求样本频率分布表中a,b的值,并根据上述频率分布表,在答题卡中作出样本频率分布直方图;
(Ⅱ)用样本估计总体,估计这个班这次数学成绩的平均数.(同一组中的数据用该组区间的中点值作代表)
| 分数 | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 2 | 8 | 12 | a | 6 | 2 |
| 频率 | 0.05 | 0.20 | 0.30 | b | 0.15 | 0.05 |

(Ⅱ)用样本估计总体,估计这个班这次数学成绩的平均数.(同一组中的数据用该组区间的中点值作代表)