题目内容
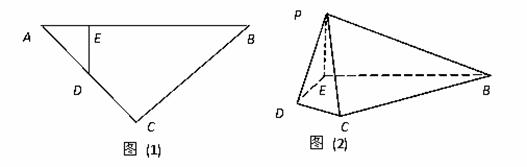
如图(1),等腰直角三角形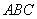 的底边
的底边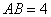 ,点
,点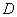 在线段
在线段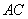 上,
上,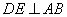 于
于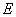 ,现将
,现将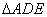 沿
沿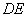 折起到
折起到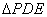 的位置(如图(2)).
的位置(如图(2)).
(Ⅰ)求证: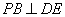 ;
;
(Ⅱ)若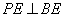 ,直线
,直线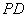 与平面
与平面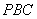 所成的角为
所成的角为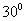 ,求
,求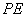 长.
长.
Ⅰ)详见解析(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)要证线线垂直,可先考虑纯线面垂直,要证线面垂直,先找出图中的线线垂直,使结论得证;(Ⅱ)为方便利用直线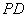 与平面
与平面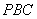 所成的角为
所成的角为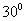 ,可建立空间直角坐标系,利用空间向量相关计算公式建立关于
,可建立空间直角坐标系,利用空间向量相关计算公式建立关于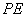 长度的方程,解之即可.
长度的方程,解之即可.
试题解析:(Ⅰ) ,
, ,
, ,
, 平面
平面 ,
,
又 ,
, ;
;
(Ⅱ) ,
,
 分别以
分别以 所在直线为
所在直线为 轴,
轴, 轴,
轴, 轴建立空间直角坐标系(如图)
轴建立空间直角坐标系(如图)


设 ,则
,则 ,
, ,
, ,
,
可得 ,
,
设平面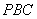 的法向量
的法向量 ,
, ,令
,令 ,可得
,可得 ,因此
,因此 是平面
是平面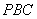 的一个法向量,
的一个法向量, ,
,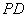 与平面
与平面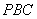 所成的角为
所成的角为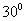 ,
, ,即
,即 ,
,
解之得: ,或
,或 (舍),因此可得
(舍),因此可得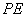 的长为
的长为 .
.
考点:直线与平面的位置关系、空间向量的应用.

练习册系列答案
相关题目
 垂直,并且与原点的距离是5的直线的方程.
垂直,并且与原点的距离是5的直线的方程.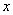 、
、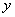 分别表示化学、物理成绩. 例如:表中化学成绩为B等级的共有20+18+4=42人.已知
分别表示化学、物理成绩. 例如:表中化学成绩为B等级的共有20+18+4=42人.已知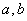 的值;
的值;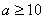 ,
,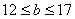 , 随机变量
, 随机变量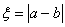 ,求
,求 的
的 上一点到直线
上一点到直线 的距离最短的点的坐标是 ( )
的距离最短的点的坐标是 ( ) ) C.
) C. D.(2,4)
D.(2,4) 内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________. 中,若
中,若 ,则
,则 项和
项和 ( )
( ) C.
C. D.
D.
 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( ) B.
B.  C.
C.  D.
D. 
 ,过曲线
,过曲线 上的点
上的点 的切线方程为
的切线方程为 .
.  时有极值,求
时有极值,求 的表达式;
的表达式;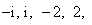 其中
其中 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).  “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率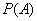 与事件
与事件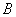 “在四次试验中,
“在四次试验中,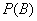 ;
;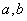 ,求随机变量
,求随机变量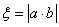 的分布列与数学期望
的分布列与数学期望