题目内容
若直线mx+2ny-4=0（m，n∈R）将圆x2+y2-4x-2y-4=0分成两段相等的弧，则m+n等于（ ）
| A、-2 | B、-1 | C、1 | D、2 |
考点：直线与圆的位置关系
专题：直线与圆
分析：由题意可得可得直线过圆心，将圆心坐标（2，1）代入直线方程化简，即可求得m+n的值．
解答：
解：由直线将圆分成等弧可得直线过圆心，将圆心坐标（2，1）代入直线mx+2ny-4=0，
可得2m+2n=4，求得：m+n=2，
故选：D．
可得2m+2n=4，求得：m+n=2，
故选：D．
点评：本题主要考查直线和圆的位置关系，判断直线过圆心，是解题的关键，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，能被5整除的个数有（ ）
| A、512 | B、192 |
| C、240 | D、108 |
函数y=2sinx（0＜x≤
）的值域是（ ）
| 2π |
| 3 |
A、（0，
| ||
B、[-
| ||
| C、[-2，2] | ||
| D、（0，2] |
把黑、红、白3张纸牌分给甲、乙、丙三人，每人一张，则事件“甲分得红牌”与“乙分得红牌”是（ ）
| A、对立事件 |
| B、必然事件 |
| C、不可能事件 |
| D、互斥但不对立事件 |
已知f（x）=cosx，则f′（
）=（ ）
| π |
| 2 |
| A、1 | B、0 | C、-1 | D、2 |
如图是“集合”的知识结构图，如果要加入“子集”，则应放在（ ）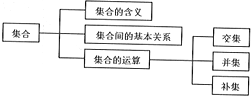
| A、“集合的含义”的下位 |
| B、“集合间的基本关系”的下位 |
| C、“交集”的下位 |
| D、“集合的运算”的下位 |
若函数y=2cos2（ωx-
）（ω＞0）的最小正周期T=
，则ω=（ ）
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |