题目内容
观察如图:则第 行的各数之和等于20132.


考点:归纳推理
专题:规律型,等差数列与等比数列
分析:第1行各数之和是(2×1-1)2,第2行各数之和是(2×2-1)2,第3行各数之和是(2×3-1)2,第4行各数之和是(2×4-1)2,故第n行各数之和是(2n-1)2,由此能求出结果.
解答:
解:观察下列数的规律图:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
知:第1行各数之和是1=12=(2×1-1)2,
第2行各数之和是2+3+4=32=(2×2-1)2,
第3行各数之和是3+4+5+6+7=52=(2×3-1)2,
第4行各数之和是4+5+6+7+8+9+10=72=(2×4-1)2,
∴第n行各数之和是(2n-1)2,
由20132=(2n-1)2,解得n=1007.
故答案为:1007
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
知:第1行各数之和是1=12=(2×1-1)2,
第2行各数之和是2+3+4=32=(2×2-1)2,
第3行各数之和是3+4+5+6+7=52=(2×3-1)2,
第4行各数之和是4+5+6+7+8+9+10=72=(2×4-1)2,
∴第n行各数之和是(2n-1)2,
由20132=(2n-1)2,解得n=1007.
故答案为:1007
点评:本题考查数列的前n项和公式的求法和应用,是基础题.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在底面是直角梯形的四棱锥S-ABCD中∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
,则这个四棱锥的体积是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
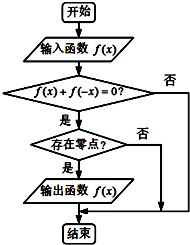
某流程图如图所示,以下四个选项中哪一个函数输入后能够被输出( )

| A、f(x)=ex-e-x | ||
| B、f(x)=x2-2 | ||
C、f(x)=
| ||
| D、f(x)=lgsinx |
已知0<α<
,sinα=
,则cos(α+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若直线mx+2ny-4=0(m,n∈R)将圆x2+y2-4x-2y-4=0分成两段相等的弧,则m+n等于( )
| A、-2 | B、-1 | C、1 | D、2 |