题目内容

在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，能被5整除的个数有（　　）
A、512B、192
C、240D、108
考点：计数原理的应用
专题：排列组合
分析：能被5整除的四位数末位是0或5的数，因此分两类，根据分类计数原理计算可得
解答： 解：能被5整除的四位数末位是0或5的数，因此分两类
第一类，末位为0时，其它三位从剩下的数中任意排3个即可，有
A
3
5
=60个，
第二类，米位为5时，首位不能排0，则首位只能从1，3，4，5选1个，第二位和第三位从剩下的任选2个即可，有
A
1
4
•A
2
4
=48个，
根据分类计数原理得可以组成60+48=108个不同的能被5整除的四位数．
故选：D
点评：本题主要考查了分类计数原理，如何分类时关键，属于中档题．
练习册系列答案
相关题目
在△ABC中，角A、B、C的对边分别为a、b、c，若b2+c2=a2+bc，且sinB•sinC=sin2A，则△ABC的形状一定是
 
．
某流程图如图所示，以下四个选项中哪一个函数输入后能够被输出（　　）
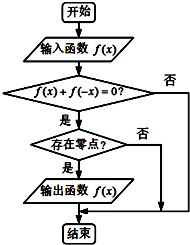
A、f（x）=ex-e-x
B、f（x）=x2-2
C、f（x）=
|x|
x
D、f（x）=lgsinx
已知0＜α＜
π
2
，sinα=
3
5
，则cos（α+
π
3
）=（　　）
A、
3-4
3
10
B、
4+3
3
10
C、
3+4
3
10
D、
4-3
3
10
若离散型随机变量X的分布列如下表，则a=（　　）
X 0 1
P 2a 0.6
A、
1
10
B、
1
5
C、
1
3
D、
1
2
在△ABC中，已知∠C=60°．a，b，c分别为∠A，∠B，∠C的对边，则
a
b+c
+
b
c+a
为（　　）
A、3-2
3
B、1
C、3-2
3
或1
D、3+2
3
设Sn是等差数列{an}的前n项和，若
a8
a3
=
1
3
，则
S15
S5
=（　　）
A、1
B、2
C、3
D、
1
3
若直线mx+2ny-4=0（m，n∈R）将圆x2+y2-4x-2y-4=0分成两段相等的弧，则m+n等于（　　）
A、-2B、-1C、1D、2
已知离散型随机变量ξ的分布列如下表所示：
ξ 0 1 2
P 0.4 p 0.3
则表中p值等于（　　）
A、0.1B、0.2
C、0.3D、0.4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网