题目内容
2.已知实数4,m,1构成一个等比数列,则曲线$\frac{x^2}{m}+{y^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$.分析 利用等比数列求出m,然后求解曲线的离心率即可.
解答 解:实数4,m,1构成一个等比数列,可得m=±2,
当m=2时,曲线$\frac{x^2}{m}+{y^2}=1$为椭圆,它的离心率为:$\frac{c}{a}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
当m=-2时,曲线$\frac{x^2}{m}+{y^2}=1$为椭双曲线,它的离心率为:$\frac{c}{a}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,
故答案为:$\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$.
点评 本题考查曲线的离心率的求法,等比数列的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数$y=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,则( )
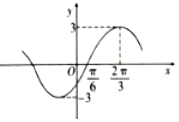

| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知a2-b2=bc,sinC=2sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
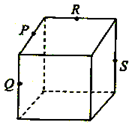

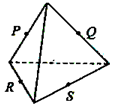
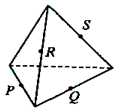
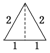
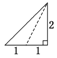
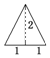
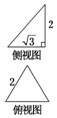 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )