题目内容
4.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其上一点P与左、右焦点F1,F2组成的三角形PF1F2的周长为2+2$\sqrt{2}$.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知直线x-$\sqrt{2}$y+n=0(n>0)与椭圆C交于不同的两点A,B,若以线段AB为直径的圆过点$M({\frac{1}{2},0})$,求△MAB的面积.
分析 (Ⅰ)椭圆的离心率及其上一点P与左、右焦点F1,F2组成的三角形PF1F2的周长为2+2$\sqrt{2}$,列出方程组求出a,c,由此能求出椭圆方程.
(Ⅱ)联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{x-\sqrt{2}y+n=0}\end{array}\right.$,得:2x2+2nx+n2-2=0,由此利用根的判别式、韦达定理、向量数量积、直线方程、点到直线距离公式、弦长公式,结合已知能求出△MAB的面积.
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其上一点P与左、右焦点F1,F2组成的三角形PF1F2的周长为2+2$\sqrt{2}$,
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{2a+2c=2+2\sqrt{2}}\end{array}\right.$,解得a=$\sqrt{2}$,c=1,
∴b2=a2-c2,解得b=1,
∴椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(Ⅱ)联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{x-\sqrt{2}y+n=0}\end{array}\right.$,消去y整理得:2x2+2nx+n2-2=0,
△=4n2-8(n2-2)>0,解得n2<4,∵n>0,∴0<n<2,①
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-n,{x}_{1}{x}_{2}=\frac{{n}^{2}-2}{2}$,
又M($\frac{1}{2}$,0),$\overrightarrow{MA}$=(${x}_{1}-\frac{1}{2},{y}_{1}$),$\overrightarrow{MB}$=(${x}_{2}-\frac{1}{2},{y}_{2}$),
由题意$\overrightarrow{MA}•\overrightarrow{MB}=0$,
∴${x}_{1}{x}_{2}-\frac{1}{2}({x}_{1}+{x}_{2})+\frac{1}{4}+{y}_{1}{y}_{2}=0$,②
又$\sqrt{2}{y}_{1}={x}_{1}+n$,$\sqrt{2}{y}_{2}={x}_{2}+n$,
∴2y1y2=${x}_{1}{x}_{2}+n({x}_{1}+{x}_{2})+{n}^{2}$,代入②,得$3{x}_{1}{x}_{2}+(n-1)({x}_{1}+{x}_{2})+{n}^{2}+\frac{1}{2}=0$,
∴3×$\frac{{n}^{2}-2}{2}$+(n-1)(-n)+n2+$\frac{1}{2}$=0,即3n2+2n-5=0,由①0<n<2,解得n=1,
直线AB方程为x-$\sqrt{2}y+1=0$,x1+x2=-1,${x}_{1}{x}_{2}=-\frac{1}{2}$,
点M到直线AB的距离d=$\frac{|\frac{1}{2}+1|}{\sqrt{1+2}}$,|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+\frac{1}{2})[(-1)^{2}+2]}$=$\frac{3\sqrt{2}}{2}$,
∴△MAB的面积S=$\frac{3\sqrt{6}}{8}$.
点评 本题考查椭圆方程、三角形面积的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、向量数量积、直线方程、点到直线距离公式、弦长公式的合理运用.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $f(x)=x-\frac{1}{x}$ | B. | f(x)=ex-1 | C. | $f(x)=x+\frac{4}{x}$ | D. | f(x)=tanx |
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
| A. | -1 | B. | 2 | C. | -2 | D. | 1 |
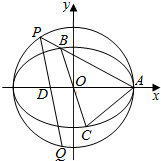 如图,在平面直角坐标系xOy中,已知圆O:x2+y2=4,椭圆C:$\frac{x^2}{4}+{y^2}=1$,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中$D(-\frac{6}{5},0)$.设直线AB,AC的斜率分别为k1,k2.
如图,在平面直角坐标系xOy中,已知圆O:x2+y2=4,椭圆C:$\frac{x^2}{4}+{y^2}=1$,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中$D(-\frac{6}{5},0)$.设直线AB,AC的斜率分别为k1,k2.