题目内容
已知椭圆C与双曲线x2-
=1的焦点相同,且与直线y=x+4有公共点,则椭圆C的长轴长的最小值为 .
| y2 |
| 3 |
考点:椭圆的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件即可设出椭圆C的方程为
+
=1,而根据椭圆C和直线y=x+4有公共点即可得到方程
+
=1有解,所以判别式△=a4-14a2+40≥0,再根据a>2,所以解该不等式即得到a2≥10,所以a的最小值为
,所以便可得到椭圆C的长轴长的最小值.
| x2 |
| a2 |
| y2 |
| a2-4 |
| x2 |
| a2 |
| (x+4)2 |
| a2-4 |
| 10 |
解答:
解:根据已知条件得到c=2,椭圆C的方程设为:
+
=1;
椭圆C与直线y=x+4有公共点;
∴方程
+
=1有解;
方程变成(
+
)x2+
x+
-1=0;
∴△=a4-14a2+40≥0;
解得a2≥10,或a2≤4;
∵a>2;
∴a2≥10;
∴椭圆C的长轴的最小值为2
.
故答案为:2
.
| x2 |
| a2 |
| y2 |
| a2-4 |
椭圆C与直线y=x+4有公共点;
∴方程
| x2 |
| a2 |
| (x+4)2 |
| a2-4 |
方程变成(
| 1 |
| a2 |
| 1 |
| a2-4 |
| 8 |
| a2-4 |
| 16 |
| a2-4 |
∴△=a4-14a2+40≥0;
解得a2≥10,或a2≤4;
∵a>2;
∴a2≥10;
∴椭圆C的长轴的最小值为2
| 10 |
故答案为:2
| 10 |
点评:考查双曲线、椭圆的标准方程,椭圆的焦点及长轴的概念,椭圆与直线有公共点时对应的方程的关系,以及一元二次方程有解时判别式△的取值情况,注意长轴的长为2a.

练习册系列答案
相关题目
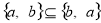 ;②
;②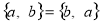 ;③
;③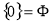 ;④
;④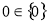 ;⑤
;⑤ ;⑥
;⑥ ,其中正确的个数为( )
,其中正确的个数为( )