题目内容
已知sinθ+cosθ=-
,求:
(1)
+
的值;
(2)tanθ的值.
| ||
| 5 |
(1)
| 1 |
| sinθ |
| 1 |
| cosθ |
(2)tanθ的值.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)已知等式两边平方,利用完全平方公式及同角三角函数间的基本关系化简,整理求出sinθcosθ的值,原式通分并利用同分母分式的加法法则计算,将各自的值代入计算即可求出值;
(2)由sinθcosθ的值,求出
的值,利用同角三角函数间的基本关系弦化切,求出tanθ的值即可.
(2)由sinθcosθ的值,求出
| 1 |
| sinθcosθ |
解答:
解:(1)把sinθ+cosθ=-
,
两边平方得:(sinθ+cosθ)2=1+2sinθcosθ=
,即sinθcosθ=-
,
则原式=
=
=
;
(2)∵sinθcosθ=-
<0,
∴
=
=
=-
,
解得:tanθ=-
或tanθ=-3.
| ||
| 5 |
两边平方得:(sinθ+cosθ)2=1+2sinθcosθ=
| 2 |
| 5 |
| 3 |
| 10 |
则原式=
| sinθ+cosθ |
| sinθcosθ |
-
| ||||
-
|
2
| ||
| 3 |
(2)∵sinθcosθ=-
| 3 |
| 10 |
∴
| 1 |
| sinθcosθ |
| sin2θ+cos2θ |
| sinθcosθ |
| tan2θ+1 |
| tanθ |
| 10 |
| 3 |
解得:tanθ=-
| 1 |
| 3 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
若复数z=
(a∈R),则在复平面内,“a<4”是“z对应点在第一象限”的( )
| a+4i |
| 1+i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知点A、B、C、D均在球O上,AB=BC=
,AC=3,若三棱锥D-ABC体积的最大值为
,则球O的表面积为( )
| 3 |
3
| ||
| 4 |
| A、36π | ||
| B、16π | ||
| C、12π | ||
D、
|
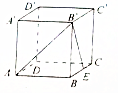 如图所示,在棱长为1的正方体ABCD-A′B′C′D′中,E为棱BC的中点.
如图所示,在棱长为1的正方体ABCD-A′B′C′D′中,E为棱BC的中点.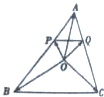 如图,O是△ABC内一点,PQ∥BC,且
如图,O是△ABC内一点,PQ∥BC,且