题目内容
设函数 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)当 时,
时, 恒成立,求实
恒成立,求实 的取值范围.
的取值范围.
 .
.(Ⅰ)当
 时,解不等式
时,解不等式 ;
;(Ⅱ)当
 时,
时, 恒成立,求实
恒成立,求实 的取值范围.
的取值范围.(I) ;(II)
;(II) 。
。
 ;(II)
;(II) 。
。本试题主要是考查了绝对值不等式的求解以及不等式恒成立问题的综合运用。
(1)因为 时,
时, ,即
,即 ,对于x分类讨论得到解集。
,对于x分类讨论得到解集。
(2)当 时,
时,
即 恒成立,
恒成立,
得 在
在 上恒成立。
上恒成立。
而 在
在 上为增函数,借助于函数的单调性得到。
上为增函数,借助于函数的单调性得到。
解:(I) 时,
时, ,即
,即 ,
,
当 时,
时, 解得
解得
又 ,
, ;
;
当 时,
时, ,解得
,解得
又 ,
,
当 时,
时, 解得
解得
又 ,
,
综上,原不等式的解集为 ………………………6分
………………………6分
(II) 当 时,
时,
即 恒成立,
恒成立,
得 在
在 上恒成立。
上恒成立。
而 在
在 上为增函数,
上为增函数,
故
 当且仅当
当且仅当 即
即 时等号成立。
时等号成立。
故 ……………………………………………………12分
……………………………………………………12分
(1)因为
 时,
时, ,即
,即 ,对于x分类讨论得到解集。
,对于x分类讨论得到解集。(2)当
 时,
时,
即
 恒成立,
恒成立,得
 在
在 上恒成立。
上恒成立。而
 在
在 上为增函数,借助于函数的单调性得到。
上为增函数,借助于函数的单调性得到。解:(I)
 时,
时, ,即
,即 ,
,当
 时,
时, 解得
解得
又
 ,
, ;
;当
 时,
时, ,解得
,解得
又
 ,
,
当
 时,
时, 解得
解得
又
 ,
,
综上,原不等式的解集为
 ………………………6分
………………………6分(II) 当
 时,
时,
即
 恒成立,
恒成立,得
 在
在 上恒成立。
上恒成立。而
 在
在 上为增函数,
上为增函数,故

 当且仅当
当且仅当 即
即 时等号成立。
时等号成立。故
 ……………………………………………………12分
……………………………………………………12分
练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
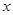 的不等式
的不等式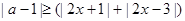 的解集非空,则实数
的解集非空,则实数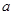 的取值范
的取值范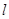 的参数方程是
的参数方程是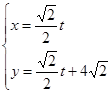 (其中
(其中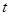 为参数),圆
为参数),圆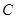 的极坐标方程为
的极坐标方程为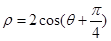 ,过直线上的点向圆引切线,则切线长的最小值是 .
,过直线上的点向圆引切线,则切线长的最小值是 .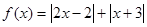
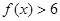 ;
;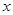 的不等式
的不等式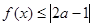 的解集不是空集,求
的解集不是空集,求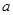 得取值范围.
得取值范围.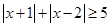
 =
= + 1.
+ 1.
 ;
;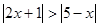 的解集是 .
的解集是 .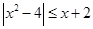 的解集是
的解集是