题目内容

已知a≠0，函数y=-acos2x-
3
asin2x+2a+b，x∈[0，
π
2
]，若函数值域为[-5，1]，求常数a，b的值．
考点：三角函数的最值
专题：三角函数的求值
分析：函数即y=-2asin（2x+
π
6
）+2a+b，由x∈[0，
π
2
]可得sin（2x+
π
6
）∈[-
1
2
，1]，再分a＞0和a＜0两种情况，分别求得常数a，b的值．
解答： 解：函数y=-acos2x-
3
asin2x+2a+b=-2asin（2x+
π
6
）+2a+b，
当x∈[0，
π
2
]时，∴2x+
π
6
∈[
π
6
，
7π
6
]，sin（2x+
π
6
）∈[-
1
2
，1]，
当a＞0时，由题意可得
-2a(-
1
2
)+2a+b=1
-2a+2a+b=-5
，求得
a=2
b=-5
．
当a＜0时，由题意可得
-2a+2a+b=1
-2a(-
1
2
)+2a+b=-5
，求得
a=-2
b=1
．
综上可得，
a=2
b=-5
，或
a=-2
b=1
．
点评：本题主要考查三角恒等变换，正弦函数的定义域和值域，属于基础题．
练习册系列答案
相关题目
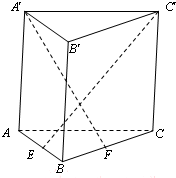如图，直三棱柱ABC-A′B′C′的侧棱长为3，AB⊥BC，且AB=BC=3，点E，F分别是棱AB，BC上的动点，且AE=BF，
（Ⅰ）求证A′F⊥C′E；
（Ⅱ）当三棱锥B′-EBF的体积取得最大值时，求二面角B′-EF-B的正切值．
已知函数f（x）=x3-
1
2
x2-2x，当x∈[-1，2]时，f（x）＜m恒成立，求实数m的取值范围．
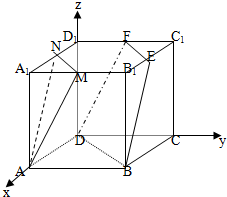如图，在正方体ABCD-A1B1C1D1中，M、N分别是棱A1B1、A1D1的中点，E、F分别是棱B1C1、C1D1的中点．求证：
（1）BD∥EF；
（2）BD⊥面A A1 C1C．
（3）平面AMN∥平面BDFE．
给出如下列联表
患心脏病患其它病合  计
高血压201030
不高血压305080
合  计5060110
由以上数据判断高血压与患心脏病之间在多大程度上有关系？
参考公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

参考数据：P（K2≥6.635）=0.010，P（K2≥7.879）=0.005．
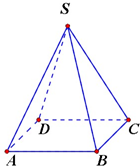若正四棱锥底面边长为a，侧棱与底面成60°角，求：
（1）棱锥的侧棱和斜高；
（2）棱锥的侧面和底面所成的角．
已知函数f（x）=alnx-x+
1
x
，g（x）=x2+x-b．y=f（x）图象恒过定点P，且P点既在y=g（x）图象上，又在y=f（x）的导函数的图象上．
（Ⅰ）求a、b的值；
（Ⅱ）设h（x）=
f(x)
g(x)
，求证：当x＞0且x≠1时，h（x）＜0；
（Ⅲ）求证：1+
1
2
+
1
3
+…+
1
n
＞lnn+
n+1
2n
（n≥2且n∈N*）．
若两个等差数列{an}、{bn}的前Sn项和分别为Sn、Tn，对任意的n∈N*都有
Sn
Tn
=
2n-1
4n-3
，则
a5
b7
=
 
．
极坐标方程为9ρ2+16ρ2sin2θ-225=0的曲线的离心率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网