题目内容
已知数列 满足
满足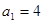 ,
, ,数列
,数列 满足
满足 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)设 ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值.
(1)详见解析;(2)2,3.
解析试题分析:(1)要证明数列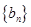 是等差数列,只需证明
是等差数列,只需证明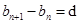 即可,而由条件中
即可,而由条件中 ,
, ,可得
,可得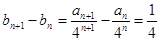 ,从而得证;(2)由(1),可以求得
,从而得证;(2)由(1),可以求得 的通项公式,结合
的通项公式,结合 ,即可求得
,即可求得 的通项公式,从而可以得到
的通项公式,从而可以得到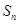 =
=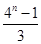 ,解关于n的不等式,即可得到满足不等式的所有整数值.
,解关于n的不等式,即可得到满足不等式的所有整数值.
(1)由 ,得
,得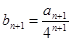 ,∴
,∴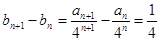 (4分)
(4分)
∴数列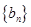 是等差数列,首项
是等差数列,首项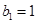 ,公差为
,公差为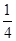 . (6分);
. (6分);
(2)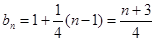 ,则
,则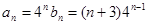 (8分)
(8分)
从而有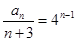 ,故
,故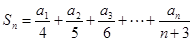
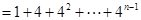
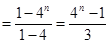 (10分)
(10分)
则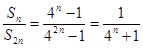 ,由
,由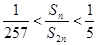 ,得
,得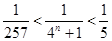 ,即
,即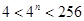 ,得
,得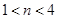 .
.
故满足不等式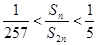 的所有正整数
的所有正整数 的值为
的值为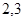 .
.
考点:1、等差数列的证明;2、等比数列前n项和.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
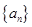 满足:
满足: .
.
 的首项
的首项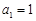 ,
, 是
是 项和,且
项和,且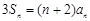
 .
.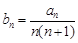 ,求数列
,求数列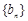 的通项公式;
的通项公式;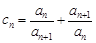 ,证明:
,证明: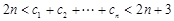 ,
,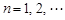 .
. 中各项均为正,有
中各项均为正,有 ,
, ,
, 中,
中, ,点
,点 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和 ;
; ,求数列
,求数列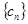 的前n项和
的前n项和 .
.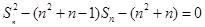
 ,数列{bn}的前n项和为Tn.证明:对于任意n
,数列{bn}的前n项和为Tn.证明:对于任意n 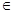 N*,都有Tn<
N*,都有Tn<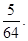
 千元时多卖出
千元时多卖出 件。
件。 与n的函数关系式;
与n的函数关系式; 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?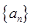 的前
的前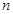 项和
项和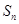 ,且满足
,且满足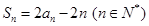 .
.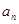 .
.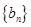 满足
满足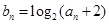 ,
,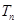 为数列{
为数列{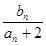 }的前
}的前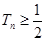 .
.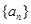 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为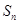 ,对于任意正整数m,n,
,对于任意正整数m,n, 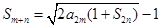 恒成立.
恒成立. 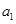 =1,求
=1,求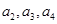 及数列
及数列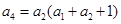 ,求证:数列
,求证:数列