题目内容
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利a元的前提下,可卖出b件;若做广告宣传,广告费为n千元比广告费为 千元时多卖出
千元时多卖出 件。
件。
(1)试写出销售量 与n的函数关系式;
与n的函数关系式;
(2)当 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
(1)
 (2)
(2)
解析试题分析:
(1)根据若做广告宣传,广告费为n千元比广告费为 千元时多卖出
千元时多卖出 件,可得
件,可得 ,利用叠加法可求得
,利用叠加法可求得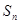 .
.
(2)根据题意在 时,利润
时,利润 ,可利用
,可利用 求最值.
求最值.
试题解析:
(1)设 表示广告费为0元时的销售量,由题意知
表示广告费为0元时的销售量,由题意知 ,
,
由叠加法可得 即为所求。
即为所求。
(2)设当 时,获利为
时,获利为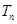 元,
元,
由题意知, ,
,
欲使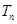 最大,则
最大,则 ,易知
,易知 ,此时
,此时 .
.
考点:叠加法求通项, 求最值.
求最值.

练习册系列答案
相关题目
 的前n项和为
的前n项和为 则三点
则三点 共线;
共线; ”的否定是“
”的否定是“ ”;
”; 在(0,1)没有零点,则k的取值范围是
在(0,1)没有零点,则k的取值范围是
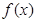 是定义在R上的奇函数,
是定义在R上的奇函数, 的解集为(
的解集为( 2,2)
2,2)
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第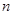 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数. ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
; 是等比数列,并用
是等比数列,并用 ;
; 满足
满足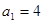 ,
, ,数列
,数列 满足
满足 .
. ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值. ,an=
,an= (
(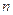 为正整数),
为正整数), ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,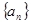 中,若
中,若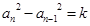 (
(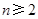 ,
,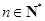 ,
,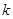 为常数),则称
为常数),则称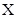 数列.
数列.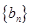 是
是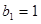 ,
,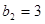 ,写出所有满足条件的数列
,写出所有满足条件的数列 项;
项; 或
或 ;
;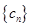 满足
满足 ,
,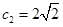 ,
,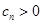 ,设数列
,设数列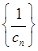 的前
的前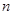 项和为
项和为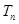 .是否存在
.是否存在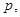
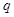 ,使不等式
,使不等式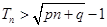 对一切
对一切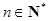 都成立?若存在,求出
都成立?若存在,求出 满足
满足 (
( ).
). 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,求
,求 中,
中, .
. 是等比数列,并求
是等比数列,并求 ;
; 满足
满足 ,数列
,数列 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.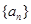 的前
的前 项和为
项和为 ,若
,若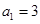 ,点
,点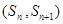 在直线
在直线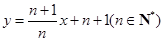 上.
上.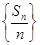 是等差数列;
是等差数列;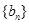 满足
满足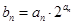 ,求数列
,求数列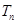 ;
;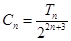 ,求证:
,求证: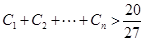 .
.