题目内容
7.若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=x2+3x+1,则f(x)=( )| A. | x2 | B. | 2x2 | C. | 2x2+2 | D. | x2+1 |
分析 利用奇偶函数性质得到f(-x)=f(x),g(-x)=-g(x),代入已知等式得到关系式,与已知等式联立即可求出f(x).
解答 解:∵定义在R上的偶函数f(x)和奇函数g(x),
∴f(-x)=f(x),g(-x)=-g(x),
代入已知等式f(x)+g(x)=x2+3x+1①,得:f(-x)+g(-x)=x2-3x+1,即f(x)-g(x)=x2-3x+1②,
联立①②,解得:f(x)=x2+1,
故选:D.
点评 此题考查了函数奇偶性的性质,熟练掌握函数奇偶性的性质是解本题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
17.在矩形ABCD中,AB=8,BC=6,沿AC将矩形ABCD折成一个45°的二面角B-AC-D,则四面体ABCD的外接球的体积为( )
| A. | $\frac{375π}{4}$ | B. | 100π | C. | $\frac{250\sqrt{2}π}{3}$ | D. | $\frac{500π}{3}$ |
18.已知数列{an}满足a1=$\frac{1}{4}$,an+1=1-$\frac{1}{a_n}$,则a2015的值为( )
| A. | $\frac{1}{4}$ | B. | -3 | C. | $\frac{2}{3}$ | D. | -2 |
15.盒中有5值LED节能灯,其中有2只是坏的,现从盒中随机地抽取2只,那么$\frac{3}{5}$是( )
| A. | 2只全是坏的概率 | B. | 2中全是好的概率 | ||
| C. | 恰有1只是坏的概率 | D. | 至少1只是坏的概率 |
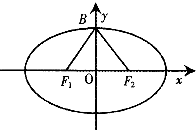 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.