题目内容
16.已知a,b为正数,且满足2<a+2b<4,那么3a-b的取值范围是(-2,12).分析 先求出满足条件的平面区域,得到点P在c处时取到最小值,在D处时取到最大值.
解答 解:以a为横坐标、b为纵坐标,在aob坐标系中作出不等式2<a+2b<4表示的平面区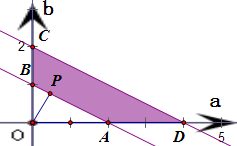 域,
域,
得到如图的四边形ABCD内部,(不包括边界),
其中A(2,0),B(0,1),C(0,2),D(4,0),
设P(a,b)为区域内一个动点,
显然p点在C(0,2)时,a最小,b最大,此时3a-b=-2,
p点在D(4,0)处时,a最大,b最小,此时3a-b=12,
故答案为:(-2,12).
点评 本题考查了简单的线性规划问题,考查了数形结合思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=x2+3x+1,则f(x)=( )
| A. | x2 | B. | 2x2 | C. | 2x2+2 | D. | x2+1 |
11.函数f(x)=$\frac{1}{3}$x3+x在点处(1,$\frac{4}{3}$)的切线与坐标轴围成的三角形的面积为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{9}$ |
1.命题“?x0∈R,x2+3x+2≤0”的否定是( )
| A. | “?x∈R,x2+3x+2>0” | B. | “?x0∉R,x2+3x+2≤0” | ||
| C. | “?x∈R,x2+3x+2≤0” | D. | “?x0∈R,x2+3x+2>0” |
5.设集合Sn={1,2,3,…,n},若Z是Sn的子集,把Z中的所有数的和称为Z的“容量”(规定空集的容量为0).若Z的容量为奇(偶)数,则称Z为Sn的奇(偶)子集.
命题①:Sn的奇子集与偶子集个数相等;
命题②:当n≥3时,Sn的所有奇子集的容量之和与所有偶子集的容量之和相等
则下列说法正确的是( )
命题①:Sn的奇子集与偶子集个数相等;
命题②:当n≥3时,Sn的所有奇子集的容量之和与所有偶子集的容量之和相等
则下列说法正确的是( )
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
6.已知正三棱柱ABC-A1B1C1(侧棱AA1⊥底面A1B1C1,底面△A1B1C1是正三角形)内接于球O,AB1与底面A1B1C1所成的角是45°,若正三棱柱ABC-A1B1C1的体积是2$\sqrt{3}$cm3,则球O的表面积是( )
| A. | $\frac{28π}{3}$cm2 | B. | $\frac{14π}{3}$cm2 | C. | $\frac{56π}{3}$cm2 | D. | $\frac{7π}{3}$cm2 |
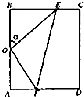 某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)