��Ŀ����
17��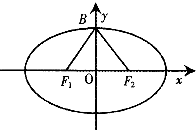 ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬BΪ�����һ���˵㣬�ҡ�F1BF2�DZ߳�Ϊ2�ĵȱ������Σ�
��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬BΪ�����һ���˵㣬�ҡ�F1BF2�DZ߳�Ϊ2�ĵȱ������Σ���1������ԲC�ı����̣�
��2������ԲC����������˵�ΪM��-a��0����N��a��0������P��x0��y0��ʹ��ֱ��PM��ֱ��PN��б��֮��Ϊ-$\frac{{b}^{2}}{{a}^{2}}$��֤������P����ԲC�ϣ�
���� ��1��ͨ����F1BF2�DZ߳�Ϊ2�ĵȱ������ο�֪c=|OF2|=1��������Բ�����֪2a=4�������ɵý��ۣ�
��2��ͨ����M��-a��0����N��a��0����P��x0��y0��������ʾ��ֱ��PM��PN��б�ʣ�����kPM•kPN=-$\frac{{b}^{2}}{{a}^{2}}$���㼴�ý��ۣ�
��� ��1���⣺��ͼ��֪��c=|OF2|=1��2a=|BF1|+|BF2|=2+2=4��
��a=2��
��b2=a2-c2=3��
����ԲC�ı������ǣ�$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2��֤������M��-a��0����N��a��0����P��x0��y0����
��ֱ��PM��PN��б�ʷֱ�ΪkPM=$\frac{{y}_{0}}{{x}_{0}+a}$��kPN=$\frac{{y}_{0}}{{x}_{0}-a}$��
�֡�ֱ��PM��ֱ��PN��б��֮��Ϊ-$\frac{{b}^{2}}{{a}^{2}}$��
��kPM•kPN=$\frac{{y}_{0}}{{x}_{0}+a}$•$\frac{{y}_{0}}{{x}_{0}-a}$=$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$��
��$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$��
���P��x0��y0������ԲC�ϣ�
���� ���⿼����Բ�ļ����ʣ��������ν�ϣ�ע����ⷽ���Ļ��ۣ������е��⣮

| A�� | x2 | B�� | 2x2 | C�� | 2x2+2 | D�� | x2+1 |
����٣�Sn�����Ӽ���ż�Ӽ�������ȣ�
����ڣ���n��3ʱ��Sn���������Ӽ�������֮��������ż�Ӽ�������֮�����
������˵����ȷ���ǣ�������
| A�� | ����ٺ�����ڶ����� | B�� | ����ٺ�����ڶ������� | ||
| C�� | ����ٳ���������ڲ����� | D�� | ����ٲ�����������ڳ��� |
��������
| A�� | 10 | B�� | -10 | C�� | $\frac{1}{5}$ | D�� | -$\frac{1}{5}$ |
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
| A�� | $\frac{28��}{3}$cm2 | B�� | $\frac{14��}{3}$cm2 | C�� | $\frac{56��}{3}$cm2 | D�� | $\frac{7��}{3}$cm2 |