题目内容
18.已知定义在(0,+∞)上的函数f(x)的导函数为f′(x),且满足xf′(x)>2f(x),若a>b>0,则( )| A. | b2f(a)<a2f(b) | B. | b2f(a)>a2f(b) | C. | a2f(a)<b2f(b) | D. | a2f(a)>b2f(b) |
分析 构造函数g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),利用导数研究其单调性即可得出.
解答 解:令g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),
g′(x)=$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)恒成立,
∴g′(x)>0,
∴函数g(x)在x∈(0,+∞)上单调递增,
∴g(a)>g(b),即$\frac{f(a)}{{a}^{2}}$>$\frac{f(b)}{{b}^{2}}$,
∴b2f(a)>a2f(b),
故选:B.
点评 本题考查了利用导数研究其单调性极值与最值、构造函数法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.若I,∅分别表示全集与空集,且(∁IP)∪M?P,则集合P,M必须满足( )
| A. | ∅?P?M | B. | M?P?I | C. | M=∅ | D. | P=I且M≠P |
13.已知集合M={x|y=$\frac{1}{\sqrt{4-2x}}$+1},集合N={y|y=-x2+4x-2},则集合M与集合N的关系为( )
| A. | M?N | B. | M?N | C. | M=N | D. | M?N |
5.若一个函数恰有两个零点,则称这样的函数为“双胞胎”函数,若函数f(x)=|ax-lnx+$\frac{a-1}{x}$|-a-3(a<0)为“双胞胎”函数,则实数a的取值范围为( )
| A. | (-$\frac{2}{3}$,+∞) | B. | (-∞,-$\frac{2}{3}$) | C. | (-$\frac{2}{3}$,0) | D. | (-1,-$\frac{2}{3}$) |
12.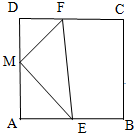 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )| A. | $[{1,\frac{5}{4}}]$ | B. | [1,2] | C. | $[{\frac{1}{2},\frac{5}{4}}]$ | D. | $[{\frac{1}{2},\frac{3}{2}}]$ |
10.设y=f(t)是某港口水的深度关于时间t(时)的函数,其中0<t≤24,下表是该港口某一天从0至24时记录的时间t与水深y的关系.
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt-φ)的图象.根据上述数据,函数y=f(t)的解析式为( )
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A. | y=12+3sin$\frac{πt}{6}$,t∈[0,24] | B. | y=12+3sin($\frac{πt}{6}$+π),t∈[0,24] | ||
| C. | y=12+3sin$\frac{πt}{12}$,t∈[0,24] | D. | y=12+3sin($\frac{πt}{12}$+$\frac{π}{2}$),t∈[0,24] |