题目内容
4.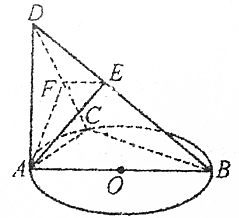 如图,AB为圆O的直径,C为圆O上的一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F,则BD与EF所成的角为90°.
如图,AB为圆O的直径,C为圆O上的一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F,则BD与EF所成的角为90°.
分析 推导出AD⊥BC,BC⊥AC,从而BC⊥面ACD,进而BC⊥AF,又AF⊥CD,从而AF⊥面BCD,进而AF⊥BD,再由AE⊥BD,得BD⊥面AEF,由此能求出BD与EF所成的角.
解答 解:AD⊥平面ABC,BC?平面ABC,∴AD⊥BC,
∵AB为圆O的直径,C为圆O上的一点,∴BC⊥AC,
∵AD∩AC=A,∴BC⊥面ACD,
∵AF?平面ACD,∴BC⊥AF,
∵AF⊥CD,BC∩CD=C,
∴AF⊥面BCD,∴AF⊥BD,
∵AE⊥BD,AF∩AE=A,
∴BD⊥面AEF,又EF?平面AEF,
∴BD⊥EF,∴BD与EF所成的角为90°.
故答案为:90°.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意线面垂直的性质的合理运用.

练习册系列答案
相关题目
16.已知函数f(x)=-2x2-kx+8在区间[1,2]上是单调函数,则k的取值范围是( )
| A. | (-∞,-8] | B. | [-8,-4] | C. | (-∞,4]∪[8,+∞) | D. | (-∞,-8]∪[-4,+∞) |
13.已知集合M={x|y=$\frac{1}{\sqrt{4-2x}}$+1},集合N={y|y=-x2+4x-2},则集合M与集合N的关系为( )
| A. | M?N | B. | M?N | C. | M=N | D. | M?N |
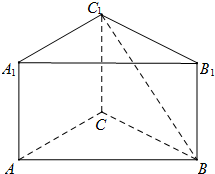 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4