题目内容
1.设函数f (x)=ex-$\frac{1}{2}$x2-x-1,函数f′(x)为f (x)的导函数.(I)求函数f′(x)的单调区间和极值;
(II)已知函数y=g (x)的图象与函数y=f (x)的图象关于原点对称,证明:当x>0时,f (x)>g (x);
(Ⅲ)如果x1≠x2,且f (x1)+f (x2)=0,证明:x1+x2<0.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间和极值即可;
(Ⅱ)令F (x)=f (x)-g (x),求出函数的导数,解关于导函数的不等式,求出F(x)>F(0),证出结论即可;
(Ⅲ)要证x1+x2<0,即证x1<-x2,根据函数的单调性只需证-f (x2)=f (x1)<f (-x2),即f (x2)+f (-x2)>0,结合(Ⅱ)得出结论.
解答 解:(I)f′(x)=ex-x-1,f′′(x)=ex-1(2分)
当x<0时,f′′(x)<0,当x>0时,f′′(x)>0
∴f′(x)在(-∞,0)上单调递减;在(0,+∞)上单调递增.
当x=0时,f′(0)=0为f′(x)极小值,无极大值.(4分)
(II)证明:由题意g (x)=-f (-x)=-e-x+$\frac{1}{2}$x2-x+1,(5分)
令F (x)=f (x)-g (x)=f (x)+f (-x)=ex+e-x-x2-2(x≥0),
F′(x)=ex-e-x-2x,F′′(x)=ex+e-x-2≥0(6分)
因此,F′(x)在[0,+∞)上单调递增,从而有F′(x)≥F′(0)=0;
因此,F (x)在[0,+∞)上单调递增,(7分)
当x>0时,有F (x)>F (0)=0,即f (x)>g (x).(8分)
(III)证明:由(I)知,f′(x)≥0,即f (x)在R上单调递增,且f (0)=0.(9分)
因为x1≠x2,不妨设x1<x2,于是有x1<0,x2>0,
要证x1+x2<0,即证x1<-x2.
因为f (x)单调递增,f (x1)+f (x2)=0
故只需证-f (x2)=f (x1)<f (-x2),即f (x2)+f (-x2)>0(10分)
因为x2>0,由(II)知上不等式成立,从而x1+x2<0成立.(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,是一道中档题.

| A. | [2,7] | B. | (0,7] | C. | [$\frac{1}{3}$,7] | D. | [3,7] |
| A. | $-\frac{i}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{i}{5}$ | D. | $\frac{1}{5}$ |
| A. | -e | B. | -1 | C. | 1 | D. | e |
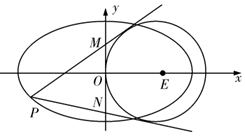 已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.
已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.