题目内容
正项数列{an}满足a1=2,点An( )在双曲线y2-x2=1上,点(bn,Tn)在直线y=-
)在双曲线y2-x2=1上,点(bn,Tn)在直线y=- x+1上,其中Tn是数列{bn}的前n项和.
x+1上,其中Tn是数列{bn}的前n项和.
①求数列{an}、{bn}的通项公式;
②设Cn=anbn,证明Cn+1<Cn
③若m-7anbn>0恒成立,求正整数m的最小值.
解:①由已知点An在y2-x2=1上知,an+1-an=1,
∴数列{an}是一个以2为首项,以1为公差的等差数列.
∴an=n+1
∵点(bn,Tn)在直线y=- x+1上
x+1上
∴Tn=- bn+1①
bn+1①
∴Tn-1=- bn-1+1②
bn-1+1②
①②两式相减得bn=- bn+
bn+ bn-1
bn-1
∴
令n=1得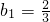
∴ ,
, .
.
∴

②
∴
=
=
= <0,
<0,
∴cn+1<cn
③∵{cn}递减而m>7cn恒成立
∴m>7c1= 而m∈N*
而m∈N*
∴m的最小值为10.
分析:①由题意知an=n+1,Tn=- bn+1,Tn-1=-
bn+1,Tn-1=- bn-1+1,所以
bn-1+1,所以 ,由此可知
,由此可知
 .
.
②由题意知 ,由此可知
,由此可知 =
= <0,所以cn+1<cn.
<0,所以cn+1<cn.
③由{cn}递减而m>7cn恒成立,知m>7c1= 而m∈N*,由此可知m的最小值为10.
而m∈N*,由此可知m的最小值为10.
点评:本题考查数列的综合运用,解题时要认真审题,仔细解答.
∴数列{an}是一个以2为首项,以1为公差的等差数列.
∴an=n+1
∵点(bn,Tn)在直线y=-
 x+1上
x+1上∴Tn=-
 bn+1①
bn+1①∴Tn-1=-
 bn-1+1②
bn-1+1②①②两式相减得bn=-
 bn+
bn+ bn-1
bn-1∴

令n=1得
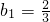
∴
 ,
, .
.∴


②

∴

=

=

=
 <0,
<0,∴cn+1<cn
③∵{cn}递减而m>7cn恒成立
∴m>7c1=
 而m∈N*
而m∈N*∴m的最小值为10.
分析:①由题意知an=n+1,Tn=-
 bn+1,Tn-1=-
bn+1,Tn-1=- bn-1+1,所以
bn-1+1,所以 ,由此可知
,由此可知
 .
.②由题意知
 ,由此可知
,由此可知 =
= <0,所以cn+1<cn.
<0,所以cn+1<cn.③由{cn}递减而m>7cn恒成立,知m>7c1=
 而m∈N*,由此可知m的最小值为10.
而m∈N*,由此可知m的最小值为10.点评:本题考查数列的综合运用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目