题目内容
(2013•江西)正项数列{an}满足
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an;
(2)令bn=
,求数列{bn}的前n项和Tn.
| a | 2 n |
(1)求数列{an}的通项公式an;
(2)令bn=
| 1 |
| (n+1)an |
分析:(1)通过分解因式,利用正项数列{an},直接求数列{an}的通项公式an;
(2)利用数列的通项公式化简bn=
,利用裂项法直接求数列{bn}的前n项和Tn.
(2)利用数列的通项公式化简bn=
| 1 |
| (n+1)an |
解答:解:(1)由正项数列{an}满足:
-(2n-1)an-2n=0,
可得(an-2n)(an+1)=0
所以an=2n.
(2)因为an=2n,bn=
,
所以bn=
=
=
(
-
),
Tn=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
数列{bn}的前n项和Tn为
.
| a | 2 n |
可得(an-2n)(an+1)=0
所以an=2n.
(2)因为an=2n,bn=
| 1 |
| (n+1)an |
所以bn=
| 1 |
| (n+1)an |
=
| 1 |
| 2n(n+1) |
=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| n+1 |
=
| n |
| 2n+2 |
数列{bn}的前n项和Tn为
| n |
| 2n+2 |
点评:本题考查数列的通项公式的求法,裂项法求解数列的和的基本方法,考查计算能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
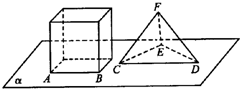 (2013•江西)如果,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )
(2013•江西)如果,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )