题目内容
根据下列各题的条件,求相应等比数列{an}中的Sn.
(1)a1=3,q=2,n=6;
(2)a1=8,q=
,n=5.
(Ⅰ)求等比数列1,2,4,…,从第5项到第10项的和;
(Ⅱ)求等比数列
,
,
,…从第3项到第7项的和.
(1)a1=3,q=2,n=6;
(2)a1=8,q=
| 1 |
| 2 |
(Ⅰ)求等比数列1,2,4,…,从第5项到第10项的和;
(Ⅱ)求等比数列
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:由等比数列的求和公式,逐个代入计算可得.
解答:
解:(1)当a1=3,q=2,n=6时,
S6=
=189;
(2)当a1=8,q=
,n=5时,
S5=
=
;
(Ⅰ)等比数列1,2,4,…,从第5项到第10项的和为:
S10-S4=
-
=1008;
(Ⅱ)等比数列
,
,
,…从第3项到第7项的和为:
S7-S2=
-
=
S6=
| 3×(1-26) |
| 1-2 |
(2)当a1=8,q=
| 1 |
| 2 |
S5=
8×(1-
| ||
1-
|
| 31 |
| 2 |
(Ⅰ)等比数列1,2,4,…,从第5项到第10项的和为:
S10-S4=
| 1×(1-210) |
| 1-2 |
| 1×(1-24) |
| 1-2 |
(Ⅱ)等比数列
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
S7-S2=
| ||||
1-
|
| ||||
1-
|
| 93 |
| 128 |
点评:本题考查等比数列的求和公式,属基础题.

练习册系列答案
相关题目
若复数z=
(a∈R),则在复平面内,“a<4”是“z对应点在第一象限”的( )
| a+4i |
| 1+i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
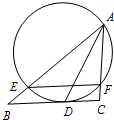 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.