题目内容
3.已知命题p:“?x0∈R,${x_0}^2+{x_0}-2>0$”,命题q:“b2=ac是a,b,c成等比数列的充要条件”.则下列命题中为真命题的是( )| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
分析 先判断命题p,q的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:当x<-2,或x>1时,${{x}_{\;}}^{2}+{x}_{\;}-2>0$,故命题p为真命题;
b2=ac=0时,a,b,c不是等比数列,帮命题q为假命题;
故命题p∧q,(¬p)∧q,(¬p)∧(¬q)均为假命题;
p∧(¬q)为真命题;
故选:C
点评 本题以命题的真假判断与应用为载体,考查了存在性问题,等比数列的定义,充要条件,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知A(3,0),B(0,4),△AOB绕y轴旋转一周得到的几何体的表面积和体积分别是( )
| A. | 9π,12π | B. | 12π,9π | C. | 24π,12π | D. | 15π,36π |
4.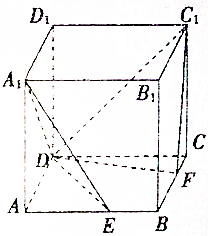 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{6}}{5}$ |
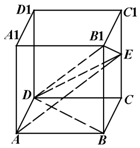 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.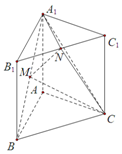 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.