题目内容
5.已知A(1,-1),B(3,0),C(2,4)三点,求平行四边形ABCD的顶点D的坐标.分析 把平行四边形转化为向量相等即可解决.
解答 解:设D点的坐标为(x,y),
∵四边形ABCD为平行四边形,
∴$\overrightarrow{AB}$=$\overrightarrow{DC}$,
∵$\overrightarrow{AB}$=(3,0)-(1,-1)=(2,1).
$\overrightarrow{DC}$=(2,4)-(x,y)=(2-x,4-y).
由向量相等的定义可得,$\left\{\begin{array}{l}{2-x=2}\\{1=4-y}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$,
即点D的坐标为(0,3).
点评 本题为向量的坐标运算以及向量相等的意义,也利用利用中点坐标公式求解,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知a,b∈(0,+∞),则下列不等式中不成立的是( )
| A. | a+b+$\frac{1}{\sqrt{ab}}$≥2$\sqrt{2}$ | B. | (a+b)($\frac{1}{a}$+$\frac{1}{b}$)≥4 | C. | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$≥2$\sqrt{ab}$ | D. | $\frac{2ab}{a+b}$>$\sqrt{ab}$ |
9.若集合A={1,2,3,4,5},集合B={x|x(4-x)<0},则图中阴影部分表示( )
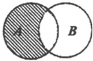

| A. | {1,2,3,4} | B. | {1,2,3} | C. | {4,5} | D. | {1,4} |