题目内容
已知tanA=3，求sin2A-2sinAcosA+1的值．
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：由题意，可将sin2A-2sinAcosA+1变为
+1，再利用商数关系将其用切表示出来，代入正切的值即可求出分式的值
| sin2A-2sinAcosA |
| sin2A+cos2A |
解答：
解：∵sin2A-2sinAcosA+1=
+1=
+1，
又tanA=3，
∴sin2A-2sinAcosA+1=
+1=
．
| sin2A-2sinAcosA |
| sin2A+cos2A |
| tan2A-2tanA |
| tan2A+1 |
又tanA=3，
∴sin2A-2sinAcosA+1=
| 9-6 |
| 9+1 |
| 13 |
| 10 |
点评：本题考查同角三角函数的关系，已知角的正切值，求解时注意“1”的妙用
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0，|φ|＜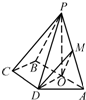
如图，已知四棱锥P-ABCD，底面ABCD是等腰梯形，且AB∥CD，O是AB中点，PO⊥平面ABCD，PO=CD=DA=