题目内容
已知椭圆![]() (a>b>0)的一个顶点为A(0,1),且它的离心率与双曲线
(a>b>0)的一个顶点为A(0,1),且它的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(I)求椭圆的方程:
(Ⅱ)过A点且斜率为k的直线与椭圆相交于A、B两点,点M在椭圆上,并且满足OM=![]() OA+
OA+![]() OB,求k的值.
OB,求k的值.
解:(I)双曲线![]() 的离心率为
的离心率为![]() .∴椭圆的离心率为
.∴椭圆的离心率为![]()
∵椭圆![]() (a>b>0)的一个顶点为A(0,1),∴b=1.
(a>b>0)的一个顶点为A(0,1),∴b=1.
∴![]() ∴
∴![]() ∴椭圆的方程为
∴椭圆的方程为![]()
(Ⅱ)过A点且斜率为k的直线的方程是y=kx+1,代入到椭圆方程中,消去y并整理得(1+4k2)x2+8kx=0.
显然这个方程有两解.设A(x1,y1),B(x2,y2),M(x,y),则可解得
![]() ,
,![]() ∴
∴![]() ,
, ![]()
即A(0,1), B(![]() ,
,![]() )
)
∴![]() (
(![]() ,
,![]() )
)
∴![]() ,
, ![]()
将E点的坐标代入到椭圆方程中,并去分母可得
![]()
展开整理得 ![]() ∴
∴ ![]()
方法二:
(Ⅱ)过A点且斜率为k的直线的方程是y=kx+1,代入到椭圆方程中,消去y并整理得(1+4k2)x2+8kx=0.①
显然这个方程有两解.设A(x1,y1),B(x2,y2),M(x,y),则
![]()
![]()
![]() ∵OM=
∵OM=![]() OA+
OA+![]() OB ∴(x,y)=
OB ∴(x,y)= ![]() (x1,y1)+
(x1,y1)+ ![]() (x2,y2)
(x2,y2)
∴![]() ,
, ![]()
∵点M在C上,∴![]()
∴![]()
∴![]()
∴![]() , 即
, 即![]() .②
.②
又由①式知:![]() ,
, ![]() , 代入②式得
, 代入②式得![]() ,
, ![]()

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
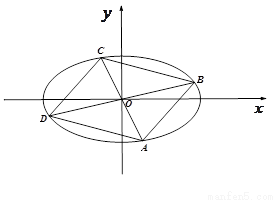
(1)求 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:

|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;
的标准方程;
(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线









 (a>b>0)的左、右焦点分别为Fl vF2
,离心率
(a>b>0)的左、右焦点分别为Fl vF2
,离心率 ,A为右顶点,K为右准线与x轴的交点,且
,A为右顶点,K为右准线与x轴的交点,且 .
. 的垂心?若存在,求出l的方程;若不存在,请说明理由.
的垂心?若存在,求出l的方程;若不存在,请说明理由.