题目内容
已知椭圆 (a>b>0)的左、右焦点分别为Fl vF2
,离心率
(a>b>0)的左、右焦点分别为Fl vF2
,离心率 ,A为右顶点,K为右准线与x轴的交点,且
,A为右顶点,K为右准线与x轴的交点,且 .
.
(1) 求椭圆的标准方程
(2) 设椭圆的上顶点为B,问是否存在直线l,使直线l交椭圆于C,D两点,且椭圆的左焦点F1恰为 的垂心?若存在,求出l的方程;若不存在,请说明理由.
的垂心?若存在,求出l的方程;若不存在,请说明理由.
(Ⅰ)设焦点坐标为F1(-c,0),F2(c,0),
由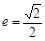 ,得
,得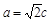 . ①
. ①
由题知 A(a,0),K(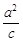 ,0),
,0),
∴ 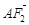 =(c-a,0),
=(c-a,0),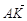 =(
=(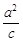 -a,0),
-a,0),
由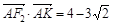 得
得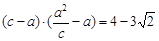 ②
②
由①、②解得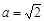 ,c=1,从而b2=a2-c2=1,即b=1.
,c=1,从而b2=a2-c2=1,即b=1.
∴ 椭圆方程为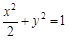 .……………………………………………………5分
.……………………………………………………5分
(Ⅱ)假设存在直线l满足题意,B(0,1),F1(-1,0),
于是直线F1B的斜率为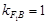 .
.
由于BF1⊥CD,令l:y=-x+m,代入x2+2y2=2整理,得
3x2-4mx+2m2-2=0.
令C(x1,y1),D(x2,y2),则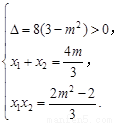
又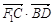 =(x1+1,y1)·(x2,y2-1)
=(x1+1,y1)·(x2,y2-1)
=x1x2+x2+y1y2-y1
=x1x2+x2+(m-x1)(m-x2)-(m-x1)
=2x1x2+m2-m(x1+x2)-m+(x1+x2)
=2x1x2 +(1-m)(x1+x2) +m2-m,
由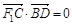 ,代入x1+x2,x1x2得
,代入x1+x2,x1x2得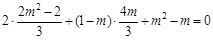 ,
,
整理得3m2+m-4=0,
解得m=1或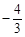 . ……………………………………………………………11分
. ……………………………………………………………11分
当m=1时,直线l恰过B点,于是B、C、D不构成三角形,故m=1舍去.
当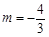 的,满足Δ=8(3-m2)>0.
的,满足Δ=8(3-m2)>0.
故所求的直线l为: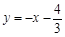 ,即3x+3y+4=0.
,即3x+3y+4=0.
【解析】略

已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆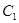 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
已知椭圆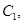
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:

|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;
的标准方程;
(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
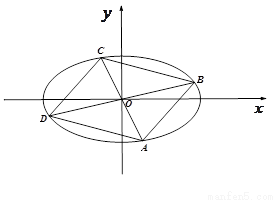
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线








