题目内容
已知椭圆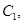
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:

|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;
的标准方程;
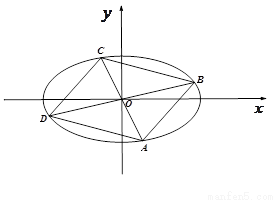
(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
【答案】
(1)
(2)
【解析】
试题分析:解析:
(2)设直线AB的方程为 ,设
,设
联立 ,得
,得
 ----------①
----------①





=








当k=0(此时 满足①式),即直线AB平行于x轴时,
满足①式),即直线AB平行于x轴时, 的最小值为-2.
的最小值为-2.
又直线AB的斜率不存在时 ,所以
,所以 的最大值为2.
11分
的最大值为2.
11分
(ii)设原点到直线AB的距离为d,则

 .
13分
.
13分
考点:直线与椭圆,抛物线
点评:主要是考查直线与椭圆以及抛物线的位置关系的运用,属于中档题。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆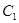 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;





 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线




 (a>b>0)的左、右焦点分别为Fl vF2
,离心率
(a>b>0)的左、右焦点分别为Fl vF2
,离心率 ,A为右顶点,K为右准线与x轴的交点,且
,A为右顶点,K为右准线与x轴的交点,且 .
. 的垂心?若存在,求出l的方程;若不存在,请说明理由.
的垂心?若存在,求出l的方程;若不存在,请说明理由.