题目内容
已知f(x)是定义在(0,+∞)上的函数,当x>1时,f(x)都满足f(x)<0,对任意正实数x、y都有f(xy)=f(x)+f(y).求证:f(x)在(0,+∞)上是递减函数.
考点:抽象函数及其应用
专题:证明题,函数的性质及应用
分析:由单调性的定义,设0<x1<x2,则
>1,当x>1时,f(x)满足f(x)<0,则f(
)<0,再由f(xy)=f(x)+f(y),得到f(x2)<f(x1),即可得证.
| x2 |
| x1 |
| x2 |
| x1 |
解答:
证明:设0<x1<x2,则
>1,
当x>1时,f(x)满足f(x)<0,
则f(
)<0,
由于f(xy)=f(x)+f(y),
则f(x2)=f(x1•
)=f(x1)+f(
)<f(x1),
即f(x1)>f(x2).
故f(x)在(0,+∞)上是递减函数.
| x2 |
| x1 |
当x>1时,f(x)满足f(x)<0,
则f(
| x2 |
| x1 |
由于f(xy)=f(x)+f(y),
则f(x2)=f(x1•
| x2 |
| x1 |
| x2 |
| x1 |
即f(x1)>f(x2).
故f(x)在(0,+∞)上是递减函数.
点评:本题考查抽象函数及运用,考查函数的单调性的判断,注意运用定义,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
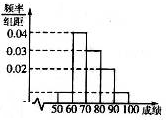 某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100).则成绩在[90,100]内的人数为( )
某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100).则成绩在[90,100]内的人数为( )