题目内容
3.已知点Q是圆M:(x+1)2+y2=64(圆心为M)上的动点,点N(1,0),线段QN的中垂线交MQ于点P(1)求动点P的轨迹E的方程;
(2)已知点B(2,2),S是轨迹E上一动点,求|SN|+|SB|的最大值;
(3)在轨迹E上是否存在点T,使$\frac{1}{|TM|}$,$\frac{1}{|MN|}$,$\frac{1}{|TN|}$成等差数列?若存在,求出|TM|与|TN|的值,若不存在,请说明理由.
分析 (1)由线段垂直平分线性质得出|PQ|=|PN|;再分析出|PM|+|PN|为定值,则知点P的轨迹为椭,最后根据椭圆的标准方程写出答案
(2)由椭圆定义|SM|+|SN|=8,于是|SN|+|SB|=8+|SB|-|SM|.
(3)利用焦半径公式,结合等差数列的性质,即可得出结论.
解答 解:(1)由题意,可知M(-1,0),|MQ|=8,
因为点P在线段NQ的垂直平分线上,所以|PQ|=|PN|
又|PM|+|PQ|=|MQ|=8,所以|PM|+|PN|=8(8>2),
那么点P的轨迹是以M、N为焦点的椭圆,其中a=4,c=1,
则b2=a2-c2=15,
所以点P的轨迹方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{15}$=1;
(2)由椭圆定义|SM|+|SN|=8,
于是|SN|+|SB|=8+|SB|-|SM|.
当M不在直线MB与椭圆交点上时,M、S、B三点构成三角形,于是|SB|-|SM|<|BF|,
而当M在直线MB与椭圆交点上时,在第一象限交点时,有|SB|-|SM|=-|BM|,
在第三象限交点时有|SB|-|SM|=|BM|.
显然当M在直线MB与椭圆第三象限交点时有最大值,其最大值为
|SN|+|SB|=8+|SB|-|SM|=8+|BM|=8+$\sqrt{(2+1)^{2}+{2}^{2}}$=8+$\sqrt{13}$.
(3)假设存在点T满足题设.
由$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{15}$=1,可知|TM|+|TN|=8,|MNA|=2,
结合$\frac{2}{|MN|}$=$\frac{1}{|TM|}$+$\frac{1}{|TN|}$.
得|TM|•|TN|=8
由$\left\{\begin{array}{l}{|TM|+|TN|=8}\\{|TM|•|TN|=8}\end{array}\right.$,得$\left\{\begin{array}{l}{|TM|=4+2\sqrt{2}}\\{|TN|=4-2\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{|TM|=4-2\sqrt{2}}\\{|TN|=4+2\sqrt{2}}\end{array}\right.$.
由于3≤|TM|≤5且3≤|TN|≤5,而4-2$\sqrt{2}$<3,4+2$\sqrt{2}$>5.
故不存在这样的点T满足题设.
点评 本题考查直线与圆的位置关系,考查椭圆的定义,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.

| A. | 3x+y-7=0 | B. | 3x-y-5=0 | C. | x+3y-5=0 | D. | x-3y+1=0 |
| A. | (3,-1,1) | B. | (3,1,-1) | C. | (3,-1,-1) | D. | (3,1,1) |
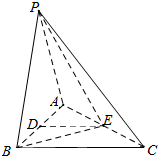 如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.
如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.


