题目内容
1.已知$f(x)=lg\frac{1-x}{1+x}$.(1)判断f(x)的奇偶性,并说明理由;
(2)设f(x)的定义域为D,a,b∈D.求$f(a)+f(b)-f(\frac{a+b}{1+ab})$的值.
分析 (1)根据函数奇偶性的定义,可得f(x)是奇函数;
(2)根据$f(x)=lg\frac{1-x}{1+x}$,结合对数的运算性质,可得$f(a)+f(b)-f(\frac{a+b}{1+ab})$的值.
解答 解:(1)由$\frac{1-x}{1+x}>0$得:
x∈(-1,1),
∴f(x)的定义域为(-1,1),关于原点对称,
又由$f({-x})+f(x)=lg\frac{1+x}{1-x}+lg\frac{1-x}{1+x}=lg1=0$,
∴f(x)是奇函数 (6分)
(2)$f(a)+f(b)-f({\frac{a+b}{1+ab}})=lg\frac{1-a}{1+a}+lg\frac{1-b}{1+b}-lg\frac{{1-\frac{a+b}{1+ab}}}{{1+\frac{a+b}{1+ab}}}$
=$lg\frac{{({1-a})}}{{({1+a})}}•\frac{{({1-b})}}{{({1+b})}}-lg\frac{1+ab-a-b}{1+ab+a+b}$
=$lg\frac{1+ab-a-b}{1+ab+a+b}-lg\frac{1+ab-a-b}{1+ab+a+b}=0$(12分)
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
10.执行如图所示的程序框图,则输出的结果是( )
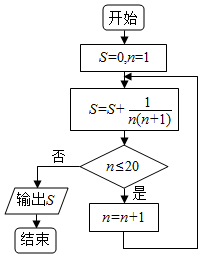

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |
11.下列问题中,应采用哪种抽样方法( )
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
| A. | 分层抽样、分层抽样、抽签法、系统抽样 | |
| B. | 分层抽样、分层抽样、随机数法、系统抽样 | |
| C. | 抽签法、分层抽样、随机数法、系统抽样 | |
| D. | 抽签法、分层抽样、系统抽样、随机数法 |