题目内容
20.已知锐角△ABC中,S△ABC=8,AB=4,AC=5,那么BC=$\sqrt{17}$.分析 利用三角形面积公式可求sinA,根据同角三角函数基本关系式可求cosA,再利用余弦定理即可求BC的值.
解答 解:∵AB=4,AC=5,S△ABC=$\frac{1}{2}$AB•AC•sinA=$\frac{1}{2}×4×5×$sinA=8,
∴解得:sinA=$\frac{4}{5}$,
∵A为锐角,可得cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{3}{5}$,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•AC•cosA}$=$\sqrt{16+25-24}$=$\sqrt{17}$.
故答案为:$\sqrt{17}$.
点评 本题主要考查了三角形面积公式,同角三角函数基本关系式,余弦定理的综合应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
11.对满足不等式组$\left\{\begin{array}{l}{x+1≥0}\\{x+y-4≤0}\\{x-y≤0}\end{array}\right.$的任意实数x,y,z=x2+y2-4x的最小值是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 6 |
8.不等式|x-3|<2的解集是( )
| A. | {x|x>5或x<1} | B. | {x|1<x<5} | C. | {x|-5<x<-1} | D. | {x|x>1} |
 中,
中, .
.
 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.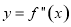 是
是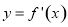 的导数.某同学经过探究发现,任意一个三次函数
的导数.某同学经过探究发现,任意一个三次函数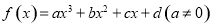 都有对称中心
都有对称中心 ,其中
,其中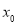 满足
满足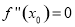 .已知函数
.已知函数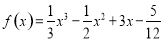 ,则
,则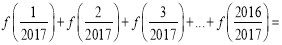 ( )
( )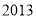 B.
B.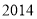 C.
C.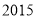 D.
D.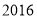
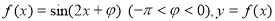 图像的一条对称轴是直线
图像的一条对称轴是直线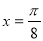 .
.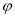 并用“五点法”画出函数
并用“五点法”画出函数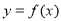 在区间
在区间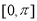 上的图像;
上的图像;