“a＜-1 是“直线ax+y-3=0的倾斜角大于$\frac{π}{4}$ 的( )A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

题目内容

15．“a＜-1”是“直线ax+y-3=0的倾斜角大于$\frac{π}{4}$”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充分必要条件		D．	既不充分也不必要条件

分析设直线ax+y-3=0的倾斜角为θ，tanθ=-a，由直线ax+y-3=0的倾斜角大于$\frac{π}{4}$，可得-a＞1或-a＜0，解得a范围即可判断出结论．

解答解：设直线ax+y-3=0的倾斜角为θ，tanθ=-a，
∵直线ax+y-3=0的倾斜角大于$\frac{π}{4}$，
∴-a＞1或-a＜0，
解得a＜-1，或a＞0．
∴“a＜-1”是“直线ax+y-3=0的倾斜角大于$\frac{π}{4}$”的充分不必要条件．
故选：A．

点评本题考查了直线的倾斜角与斜率的关系、三角函数的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案

6．

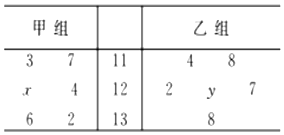如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩（单位：分），已知甲组数据的众数为124，乙组数据的平均数为甲组数据的中位数，则x，y的值分别为（　　）

3．已知直线l的参数方程为$\left\{\begin{array}{l}{x=1+2t}\\{y=-\sqrt{3}+\sqrt{3}t}\end{array}\right.$（t为参数），以原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是ρsin²θ-3cosθ=0．
（Ⅰ）求曲线C的直角坐标方程以及直线l的极坐标方程；
（Ⅱ）求直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）

10．已知实数x、y满足$\left\{\begin{array}{l}y≤x-1\\ x≤3\\ x+5y≥4\end{array}\right.$，则$\frac{x^2}{y}$的最小值是（　　）

20．某商场拟对商品进行促销，现有两种方案供选择．每种促销方案都需分两个月实施，且每种方案中第一个月与第二个月的销售相互独立．根据以往促销的统计数据，若实施方案1，顶计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4．第二个月销量是笫一个月的1.4倍和1.6倍的概率都是0.5；若实施方案2，预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3，第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4．令ξ_i（i=1，2）表示实施方案i的第二个月的销量是促销前销量的倍数．
（Ⅰ）求ξ₁，ξ₂的分布列：
（Ⅱ）不管实施哪种方案，ξ_i与第二个月的利润之间的关系如表，试比较哪种方案第二个月的利润更大．

销量倍数	ξ_i≤1.7	1.7＜ξ_i＜2.3	ξ_i2.3
利润（万元）	15	20	25

7．已知正数x，y满足x+2y-2xy=0，那么2x+y的最小值是$\frac{9}{2}$．

4．已知复数z满足z（2+i）=3+2i，则|z|=（　　）

$\frac{\sqrt{65}}{5}$

D．

$\sqrt{15}$

19．甲、乙两人可参加A，B，C三个不同的学习小组，若每人必须参加并且仅能参加一个学习小组，则两人参加同一个学习小组的概率为（　　）

试题分类