题目内容
10．已知实数x、y满足$\left\{\begin{array}{l}y≤x-1\\ x≤3\\ x+5y≥4\end{array}\right.$，则$\frac{x^2}{y}$的最小值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 设z=$\frac{x^2}{y}$，则x2=zy，作出不等式组对应的平面区域，利用数形结合即可得到结论．
解答 解：作出不等式组$\left\{\begin{array}{l}y≤x-1\\ x≤3\\ x+5y≥4\end{array}\right.$对应的平面区域如图：
由图象可知x＞0，y＞0
设z=$\frac{x^2}{y}$，则x2=zy，（z＞0），对应的曲线为抛物线，
由图象可知当直线y=x-1与抛物线相切时，此时z取得最小值，
将y=x-1代入x2=zy，得x2-zx+z=0，
由△=z2-4z=0得z=4或z=0（舍去），
故$\frac{x^2}{y}$的最小值是4，
故选：D．
点评 本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．若（1+i）2+|2i|=$\overline{z}$，其中z=a+bi（a，b∈R，i为虚数单位），则直线bx-ay+a=0的斜率为（ ）
| A． | -1 | B． | 1 | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
1．设双曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$的离心率为$\frac{{2\sqrt{3}}}{3}$，且一个焦点与抛物线x2=8y的焦点相同，则此双曲线的方程是（ ）
| A． | $\frac{y^2}{3}-{x^2}=1$ | B． | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C． | ${y^2}-\frac{x^2}{3}=1$ | D． | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
18．已知集合A={1，3}，$B=\{x|0＜lg（x+1）＜\frac{1}{2}，x∈Z\}$，则A∪B=（ ）
| A． | {1，3} | B． | {1，2，3} | C． | {1，3，4} | D． | {1，2，3，4} |
5．已知集合A={x|y=lg（x+1）}，B=$\left\{{\left.x\right|\frac{3-x}{x}＜0}\right\}$，则有（ ）
| A． | -3∈A | B． | A∩B=（-1，0） | C． | A∪B=R | D． | A?B |
15．“a＜-1”是“直线ax+y-3=0的倾斜角大于$\frac{π}{4}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
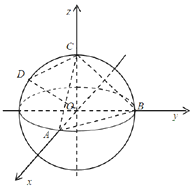如图所示，球O的球心O在空间直角坐标系O-xyz的原点，半径为1，且球O分别与x，y，z轴的正半轴交于A，B，C三点．已知球面上一点$D（{0，-\frac{{\sqrt{3}}}{2}，\frac{1}{2}}）$．