题目内容
16．若x＞-1，则函数$y=x+\frac{1}{x+1}$取最小值时对应的x的值为0．分析 变形利用基本不等式即可得出．
解答 解：∵x＞-1，∴x+1＞0．
∴函数y=x+$\frac{1}{x+1}$=x+1+$\frac{1}{x+1}$-1≥2$\sqrt{（x+1）•\frac{1}{x+1}}$-1=2-1=1，当且仅当x=0时取等号．
∴函数y=x+$\frac{1}{x+1}$的最小值为为1．
故答案为：0．
点评 本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
6．已知变量x，y满足约束条件$\left\{\begin{array}{l}x-y≥2\\ x+y≤4\\ y≥-1\end{array}\right.$，则目标函数z=x-2y的最小值为（ ）
| A． | -1 | B． | 1 | C． | 3 | D． | 7 |
7．
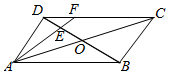在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F．若AB=2，$AD=\sqrt{2}$，∠BAD=45°，则$\overrightarrow{AF}•\overrightarrow{BE}$=（ ）
在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F．若AB=2，$AD=\sqrt{2}$，∠BAD=45°，则$\overrightarrow{AF}•\overrightarrow{BE}$=（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | -$\frac{1}{2}$ | D． | 1 |
8．若复数z满足（-3+4i）$\overline{z}$=25i，其中i为虚数单位，则z=（ ）
| A． | 4-3i | B． | 4+3i | C． | -5+3i | D． | 3+4i |
5．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递减，若实数a满足f（log3a）+f（${log}_{\frac{1}{3}}$a）≤2f（2），则a的取值范围是（ ）
| A． | [$\frac{1}{9}$，9] | B． | （-∞，$\frac{1}{9}$] | C． | [$\frac{1}{2}$，2] | D． | （0，$\frac{1}{9}$]∪[9，+∞] |
13．下列各组函数中，表示同一函数的是（ ）
| A． | f（x）=2log2x，$g（x）={log_2}{x^2}$ | B． | f（x）=|x|，$g（x）={（\sqrt{x}）^2}$ | ||
| C． | f（x）=x，$g（x）=lo{g_2}{2^x}$ | D． | f（x）=x+1，$g（x）=\frac{x^2}{x}-1$ |