题目内容
15.参考如下定义及定理,解答问题.定义:横坐标与纵坐标均为整数的点叫做整点,顶点为整点的三角形叫做整点三角形.
定理:设整点三角形内部的整点数为N,边上(包括顶点)的整点数为L,则三角形的面积为S=N+$\frac{L}{2}$-1.
问题:求满足不等式组$\left\{\begin{array}{l}{y≤2x}\\{y≥\frac{1}{2}x}\\{x+y≤30}\end{array}\right.$的整点的个数.
分析 作出不等式组对应的平面区域,求出三角形的面积以及在三角形边上的整数点的个数,结合定理求出三角形内部的整数点的公式即可得到结论.
解答 解:作出不等式组对应的平面区域如图,
由$\left\{\begin{array}{l}{y=2x}\\{x+y=30}\end{array}\right.$得$\left\{\begin{array}{l}{x=10}\\{y=20}\end{array}\right.$,即A(10,20),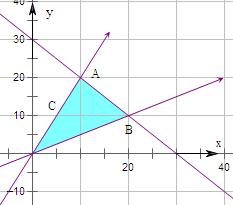
由$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{x+y=30}\end{array}\right.$得$\left\{\begin{array}{l}{x=20}\\{y=10}\end{array}\right.$,即B(20,10).
则当y=10时,由y=2x得x=5,即C(5,10),
则S△OAB=S△ABC+S△OBC=$\frac{1}{2}×$15×10+$\frac{1}{2}×$15×10=150,
当0≤x≤10时,y=2x上有11个整数点,
当1≤x≤20时,y=$\frac{1}{2}$x上有20个整数点,
当11≤x≤19时,x+y=30上有9个整数点,
则设整点三角形内部的整点数为N,边上(包括顶点)的整点数为L,
则L=11+20+9=40,
由三角形的面积为S=N+$\frac{L}{2}$-1.得N=S+1-$\frac{L}{2}$=150+1-20=129,
即满足不等式组$\left\{\begin{array}{l}{y≤2x}\\{y≥\frac{1}{2}x}\\{x+y≤30}\end{array}\right.$的整点的个数为129+40=169个.
点评 本题主要考查线性规划的应用,作出不等式组对应的平面区域结合定义和定理的关系,利用数形结合是解决本题的关键.综合性较强,考查学生的运算和推理能力.

| A. | $\frac{147}{60}$ | B. | $\frac{17}{6}$ | C. | $\frac{25}{4}$ | D. | $\frac{137}{60}$ |
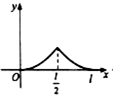
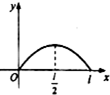
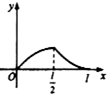
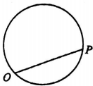 如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )
如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )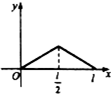
 已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上横坐标为3的点,且P到抛物线焦点F的距离等于4.
已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上横坐标为3的点,且P到抛物线焦点F的距离等于4.