题目内容
设 是锐角三角形,
是锐角三角形, 分别是内角A,B,C所对边长,并且
分别是内角A,B,C所对边长,并且
(Ⅰ)求角A的值; (Ⅱ)若 ,求
,求 (其中
(其中 ).
).
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)利用两角和与差的三角函数对等式 的右
的右
端进行变形化简,既然目标求的是 ,则必可最终消去
,则必可最终消去 .
.
(Ⅱ)根据 及
及 的值,可得关于
的值,可得关于 的一个等式;在等式
的一个等式;在等式
中,代入 和
和 可得关于
可得关于 的另一个等式,两式联立解方程组即得.
的另一个等式,两式联立解方程组即得.
试题解析:(Ⅰ)因为

(Ⅱ)由 可得
可得 ①
①
由(I)知 所以
所以 ②
②
由余弦定理知 及①代入,得
及①代入,得 ③
③
③+②×2,得 ,所以
,所以
因此,c,b是一元二次方程 的两个根.
的两个根.
解此方程并由
考点:1.三角形内的三角恒等变换;2.向量的数量积;3.余弦定理.

练习册系列答案
相关题目
 ,已知石塔的高度为
,已知石塔的高度为 .
.
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点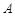 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看 )最大,求山的高度
)最大,求山的高度 中,
中, ,
, ,设
,设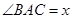 ,并记
,并记
 的解析式及其定义域;
的解析式及其定义域; ,若函数
,若函数 的值域为
的值域为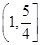 ,试求正实数
,试求正实数 的值
的值  中,设
中,设 、
、 、
、 分别为角
分别为角 、
、 、
、 的对边,角
的对边,角 交
交 边于
边于 ,
,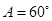 .
. ;
; ,
, ,求其三边
,求其三边 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足
 ;
; ,
, ,
, 的值.
的值. 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
,
 的值.
的值.