题目内容
在平面直角坐标系xOy中，已知点A的坐标为（3，a），a∈R，点P满足
=λ
，λ∈R，|
|•|
|=72，则线段OP在x轴上的投影长度的最大值为 ．
| OP |
| OA |
| OA |
| OP |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由点A的坐标为（3，a），可得|
|≥3，由
=λ
，利用向量共线定理可知：O，P，A三点共线．由|
||
|=72，可知|
|=
，设OP与x轴夹角为θ，则OP在x轴上的投影长度为|
|cosθ=|
|×
=
，即可得出．
| OA |
| OP |
| OA |
| OA |
| OP |
| OP |
| 72 | ||
|
|
| OP |
| OP |
| 3 | ||
|
|
| 216 | ||
|
|
解答：
解：点A的坐标为（3，a），则|
|≥3，
又
=λ
，则O，P，A三点共线，
∵|
||
|=72，则|
|=
，
设OP与x轴夹角为θ，
则OP在x轴上的投影长度为|
|cosθ=|
|
=
≤24，
即线段OP在x轴上的投影长度的最大值为24．
故答案为：24．
| OA |
又
| OP |
| OA |
∵|
| OA |
| OP |
| OP |
| 72 | ||
|
|
设OP与x轴夹角为θ，
则OP在x轴上的投影长度为|
| OP |
| OP |
| 3 | ||
|
|
| 216 | ||
|
|
即线段OP在x轴上的投影长度的最大值为24．
故答案为：24．
点评：本题考查了向量的投影定义、不等式的性质，考查了推理能力，属于中档题．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
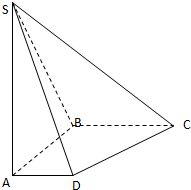如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=
如图是某算法的程序框图，若任意输入[