题目内容
函数y=f（x）在（-1，1）上是减函数，且为奇函数，满足f（a2-a-1）+f（a-2）＞0，试求a的范围．
分析：要求a的取值范围，先要列出关于a的不等式，这需要根据原条件，然后根据减函数的定义由函数值逆推出自变量的关系，通过解不等式组求出a的范围即可．
解答：解：由题意，f（a2-a-1）+f（a-2）＞0即f（a2-a-1）＞-f（a-2），
而又函数y=f（x）为奇函数，所以f（a2-a-1）＞f（2-a）．---------------（4分）
又函数y=f（x）在（-1，1）上是减函数，有
⇒
⇒1＜a＜
---------------（10分）
所以，a的取值范围是（1，
）．---------------（12分）
而又函数y=f（x）为奇函数，所以f（a2-a-1）＞f（2-a）．---------------（4分）
又函数y=f（x）在（-1，1）上是减函数，有
|
|
| 3 |
所以，a的取值范围是（1，
| 3 |
点评：本题主要考查了函数奇偶性的应用，以及单调性的应用，这两个性质是函数的重要性质，是高考的重点，属于基础题．
练习册系列答案
相关题目
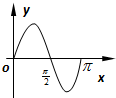
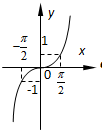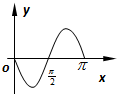
已知函数y=f（x）的图象如图，则函数
